题目内容
若函数f(x)=ax-1(a>0,a≠1)的定义域和值域都是[0,2],则实![]() 数a等于__________.
数a等于__________.
![]()
解析 由题意得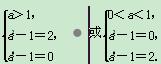
解得a=![]() .
.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
题目内容
若函数f(x)=ax-1(a>0,a≠1)的定义域和值域都是[0,2],则实![]() 数a等于__________.
数a等于__________.
![]()
解析 由题意得
解得a=![]() .
.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案