题目内容
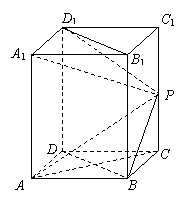 如图,在长方体
如图,在长方体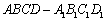
中,已知底面ABCD是边长为1的正方形,侧棱
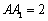 ,P是侧棱
,P是侧棱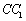 上的一点,
上的一点,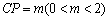 .
.
(Ⅰ)试问直线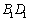 与AP能否垂直?并说明理由;
与AP能否垂直?并说明理由;
(Ⅱ)试确定m,使直线AP与平面BDD1B1所成角为60º;
(Ⅲ)若m=1,求平面PA1D1与平面PAB所成角的大小.
【答案】
(Ⅰ)以D为原点,DA、DC、DD1分别为
x、y、z轴,建立如图所示的空间直角坐标系O-xyz.
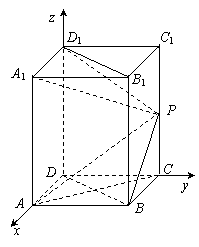 则D(0,0,0), A(1,0,0), B(1,1,0),
C(0,1,0),
则D(0,0,0), A(1,0,0), B(1,1,0),
C(0,1,0),
D1 (0,0,2),A1 (1,0,2),B1 (1,1,2),C1 (0,1,2), P(0,1,m),
所以 ,
,
 .………4分
.………4分
(Ⅱ)∵

又∵ ,
,
∴ 的一个法向量.
的一个法向量.
设直线 与平面
与平面 所成的角为
所成的角为 ,
,
则
 =
= ,解得
,解得 .
.
故当 时,直线AP与平面
时,直线AP与平面 所成角为60º.………………8分
所成角为60º.………………8分
(Ⅲ)∵m=1,∴P(0,1,1),∴ .
.
设平面PA1D1的法向量为 ,可求得
,可求得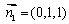 ,
,
设平面PAB的法向量为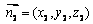 ,可求得
,可求得 .
.
∴ ,
,
故平面PA1D1与平面PAB所成角为600. ………………12分

练习册系列答案
相关题目
 如图,在长方体中,
如图,在长方体中,


 中,
中, ,
, 则
则 与平面
与平面 所成角的正弦值为 ( )
所成角的正弦值为 ( )
 B.
B. C.
C. D.
D.