题目内容
已知: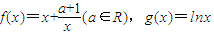 .
.(I)若f′(1)=2,求a的值;
(Ⅱ)已知a>e-1,若在[1,e](e=2.718…)上存在一点x,使得f(x)<ag(x)成立,求a的取值范围;
(Ⅲ)设函数g(x)的图象C1与函数
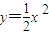 +bx的图象C2交于点A、B,过线段A、B的中点M作x轴的垂线分别交C1、C2于点P、Q,问是否存在点M使C1在P处的切线与C2在Q处的切线平行?若存在,求出M的横坐标;若不存在,请说明理由.
+bx的图象C2交于点A、B,过线段A、B的中点M作x轴的垂线分别交C1、C2于点P、Q,问是否存在点M使C1在P处的切线与C2在Q处的切线平行?若存在,求出M的横坐标;若不存在,请说明理由.
【答案】分析:(I)求导函数,利用f′(1)=2,可求a的值;
(Ⅱ)设F(x)=f(x)-ag(x)=x+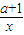 -alnx(x>0),则若在[1,e](e=2.718…)上存在一点x,使得f(x)<ag(x)成立,等价于x∈[1,e],Fmin(x)<0,由此可求a的取值范围;
-alnx(x>0),则若在[1,e](e=2.718…)上存在一点x,使得f(x)<ag(x)成立,等价于x∈[1,e],Fmin(x)<0,由此可求a的取值范围;
(Ⅲ)设A(x1,y1),B(x2,y2),且0<x1<x2,则P,Q的横坐标均为x=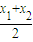 ,确定C1在P处的切线斜率为k1=
,确定C1在P处的切线斜率为k1=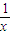 =
=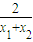 ;C2在Q处的切线斜率为k2=x+b=
;C2在Q处的切线斜率为k2=x+b=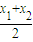 +b,假设C1在P处的切线与C2在Q处的切线平行,则k1=k2,由此可引出矛盾,故得解.
+b,假设C1在P处的切线与C2在Q处的切线平行,则k1=k2,由此可引出矛盾,故得解.
解答:解:(I)求导函数,可得f′(x)=1-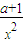
∴f′(1)=1-(a+1)=2,
∴a=-2;
(Ⅱ)设F(x)=f(x)-ag(x)=x+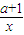 -alnx(x>0),则若在[1,e](e=2.718…)上存在一点x,使得f(x)<ag(x)成立,等价于x∈[1,e],Fmin(x)<0
-alnx(x>0),则若在[1,e](e=2.718…)上存在一点x,使得f(x)<ag(x)成立,等价于x∈[1,e],Fmin(x)<0
求导函数可得F′(x)=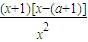
令F′(x)=0得x=a+1或x=-1(舍去)
∵a>e-1,∴x=a+1>e
∵x∈(0,a+1),F′(x)<0,函数递减
∴F(x)在[1,e]上单调递减
∴Fmin(x)=F(e)=e+
∴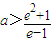
∵a>e-1,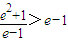 ,∴
,∴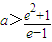
∴a的取值范围为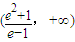 ;
;
(Ⅲ)设A(x1,y1),B(x2,y2),且0<x1<x2,则P,Q的横坐标均为x=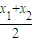
C1在P处的切线斜率为k1=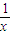 =
=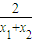 ;C2在Q处的切线斜率为k2=x+b=
;C2在Q处的切线斜率为k2=x+b=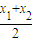 +b
+b
假设C1在P处的切线与C2在Q处的切线平行,则k1=k2,即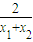 =
= +b
+b
∴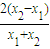 =
=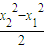 +b(x2-x1)=lnx2-lnx1,
+b(x2-x1)=lnx2-lnx1,
∴ln =
=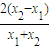 =
=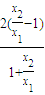
设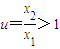 ,在lnu=
,在lnu=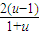 (u>1)①
(u>1)①
设h(u)=lnu-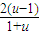 (u>1),则h′(u)=
(u>1),则h′(u)=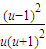
∵u>1,∴h′(u)>0
∴h(u)在[1,+∞)上单调递增,故h(u)>h(1)=0
∴lnu>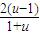
这与①矛盾,假设不成立
∴C1在P处的切线与C2在Q处的切线不平行.
点评:本题考查导数知识的运用,考查函数的单调性与最值,考查学生分析解决问题的能力,难度大.
(Ⅱ)设F(x)=f(x)-ag(x)=x+
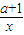 -alnx(x>0),则若在[1,e](e=2.718…)上存在一点x,使得f(x)<ag(x)成立,等价于x∈[1,e],Fmin(x)<0,由此可求a的取值范围;
-alnx(x>0),则若在[1,e](e=2.718…)上存在一点x,使得f(x)<ag(x)成立,等价于x∈[1,e],Fmin(x)<0,由此可求a的取值范围;(Ⅲ)设A(x1,y1),B(x2,y2),且0<x1<x2,则P,Q的横坐标均为x=
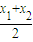 ,确定C1在P处的切线斜率为k1=
,确定C1在P处的切线斜率为k1=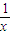 =
=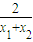 ;C2在Q处的切线斜率为k2=x+b=
;C2在Q处的切线斜率为k2=x+b=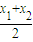 +b,假设C1在P处的切线与C2在Q处的切线平行,则k1=k2,由此可引出矛盾,故得解.
+b,假设C1在P处的切线与C2在Q处的切线平行,则k1=k2,由此可引出矛盾,故得解.解答:解:(I)求导函数,可得f′(x)=1-
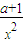
∴f′(1)=1-(a+1)=2,
∴a=-2;
(Ⅱ)设F(x)=f(x)-ag(x)=x+
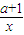 -alnx(x>0),则若在[1,e](e=2.718…)上存在一点x,使得f(x)<ag(x)成立,等价于x∈[1,e],Fmin(x)<0
-alnx(x>0),则若在[1,e](e=2.718…)上存在一点x,使得f(x)<ag(x)成立,等价于x∈[1,e],Fmin(x)<0求导函数可得F′(x)=
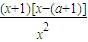
令F′(x)=0得x=a+1或x=-1(舍去)
∵a>e-1,∴x=a+1>e
∵x∈(0,a+1),F′(x)<0,函数递减
∴F(x)在[1,e]上单调递减
∴Fmin(x)=F(e)=e+

∴
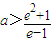
∵a>e-1,
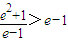 ,∴
,∴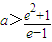
∴a的取值范围为
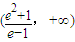 ;
;(Ⅲ)设A(x1,y1),B(x2,y2),且0<x1<x2,则P,Q的横坐标均为x=
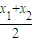
C1在P处的切线斜率为k1=
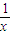 =
=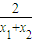 ;C2在Q处的切线斜率为k2=x+b=
;C2在Q处的切线斜率为k2=x+b=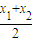 +b
+b假设C1在P处的切线与C2在Q处的切线平行,则k1=k2,即
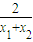 =
= +b
+b∴
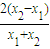 =
=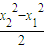 +b(x2-x1)=lnx2-lnx1,
+b(x2-x1)=lnx2-lnx1,∴ln
 =
=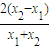 =
=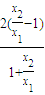
设
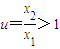 ,在lnu=
,在lnu=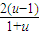 (u>1)①
(u>1)①设h(u)=lnu-
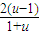 (u>1),则h′(u)=
(u>1),则h′(u)=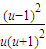
∵u>1,∴h′(u)>0
∴h(u)在[1,+∞)上单调递增,故h(u)>h(1)=0
∴lnu>
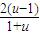
这与①矛盾,假设不成立
∴C1在P处的切线与C2在Q处的切线不平行.
点评:本题考查导数知识的运用,考查函数的单调性与最值,考查学生分析解决问题的能力,难度大.

练习册系列答案
相关题目
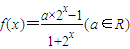 .
.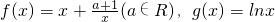 .
.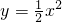 +bx的图象C2交于点A、B,过线段A、B的中点M作x轴的垂线分别交C1、C2于点P、Q,问是否存在点M使C1在P处的切线与C2在Q处的切线平行?若存在,求出M的横坐标;若不存在,请说明理由.
+bx的图象C2交于点A、B,过线段A、B的中点M作x轴的垂线分别交C1、C2于点P、Q,问是否存在点M使C1在P处的切线与C2在Q处的切线平行?若存在,求出M的横坐标;若不存在,请说明理由.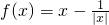 .
. .
. .
. .
. .
.