题目内容
在直角坐标系中,过双曲线 的左焦点F作圆x2+y2=1的一条切线(切点为T)交双曲线右支于P,若M为线段FP的中点,则OM-MT= .
的左焦点F作圆x2+y2=1的一条切线(切点为T)交双曲线右支于P,若M为线段FP的中点,则OM-MT= .
【答案】分析:利用双曲线的性质求出PE和OM;利用解三角形的方法把各边长MF和FT求出来进而把MT表示出来;代入即可求OM-MT的值.
解答:解:设PF=2x,则由双曲线的定义得:PE=2x-2,所以OM= =x-1,
=x-1,
又因为MT=FT-MF=FT- =
= -x=
-x= -x=3-x,
-x=3-x,
∵(3-x)2+1=(x-1)2
∴x=
故OM-MT=x-1-(3-x)=2x-4= .
.
故答案为 .
.
点评:本题主要考查双曲线的定义的应用,直线与圆的位置关系以及三角形中的有关结论.是对基础知识的综合考查,属于中档题目.
解答:解:设PF=2x,则由双曲线的定义得:PE=2x-2,所以OM=
 =x-1,
=x-1,又因为MT=FT-MF=FT-
 =
= -x=
-x= -x=3-x,
-x=3-x,∵(3-x)2+1=(x-1)2
∴x=

故OM-MT=x-1-(3-x)=2x-4=
 .
.故答案为
 .
.点评:本题主要考查双曲线的定义的应用,直线与圆的位置关系以及三角形中的有关结论.是对基础知识的综合考查,属于中档题目.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
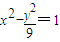 的左焦点F作圆x2+y2=1的一条切线(切点为T)交双曲线右支于P,若M为线段FP的中点,则OM-MT= .
的左焦点F作圆x2+y2=1的一条切线(切点为T)交双曲线右支于P,若M为线段FP的中点,则OM-MT= .