题目内容
11．已知关于x的方程x2+（4+i）x+4+ai=0（a∈R）有实根b，则a+b的值为（ ）| A． | 0 | B． | -1 | C． | ±1 | D． | 1 |
分析 关于x的方程x2+（4+i）x+4+ai=0（a∈R）有实根b，化为b2+4b+4+（a+b）i=0，$\left\{\begin{array}{l}{{b}^{2}+4b+4=0}\\{a+b=0}\end{array}\right.$，解出即可．
解答 解：∵关于x的方程x2+（4+i）x+4+ai=0（a∈R）有实根b，
∴b2+（4+i）b+4+ai=0，
化为b2+4b+4+（a+b）i=0，
∴$\left\{\begin{array}{l}{{b}^{2}+4b+4=0}\\{a+b=0}\end{array}\right.$，
∴a+b=0．
故选：A．
点评 本题考查了复数相等、运算法则，考查了计算能力，属于基础题．
练习册系列答案
相关题目
1．已知F是抛物线y=$\frac{1}{4}$x2的焦点，P是该抛物线上的动点，则线段PF中点的轨迹方程是（ ）
| A． | x2=2y-1 | B． | x2=2y-$\frac{1}{16}$ | C． | x2=y-$\frac{1}{2}$ | D． | x2=2y-2 |
2．已知函数f（x）=$\left\{\begin{array}{l}{{k}^{2}+2k（1-{a}^{2}），x≥0}\\{{x}^{2}-2（1-{a}^{2}）x+（a-4）^{2}，x＜0}\end{array}\right.$，a∈R，若对任意非零实数x1，存在非零实数x2（x1≠x2），使得f（x2）=f（x1），则实数k的最小值（ ）
| A． | $\frac{15}{2}$ | B． | $-\frac{15}{2}$ | C． | $-\frac{2}{3}$ | D． | $\frac{2}{3}$ |
6．
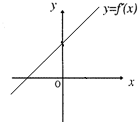函数y=f（x）的图象过原点且它的导函数y=f′（x）的图象是如图所示的一条直线，y=f（x）的图象的顶点在（ ）
函数y=f（x）的图象过原点且它的导函数y=f′（x）的图象是如图所示的一条直线，y=f（x）的图象的顶点在（ ）| A． | 第Ⅰ象限 | B． | 第Ⅱ象限 | C． | 第Ⅲ象限 | D． | 第Ⅳ象限 |
3．单位正方体（棱长为1）被切去一部分，剩下部分几何体的三视图如图所示，则（ ）
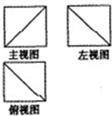
| A． | 该几何体体积为$\frac{5}{6}$ | B． | 该几何体体积可能为$\frac{2}{3}$ | ||
| C． | 该几何体表面积应为$\frac{9}{2}$+$\frac{\sqrt{3}}{2}$ | D． | 该几何体唯一 |
20．已知点P（sinα-cosα，tanα）在第二象限，则α的一个变化区间是（ ）
| A． | （-$\frac{π}{2}$，$\frac{π}{2}$） | B． | $（{-\frac{π}{4}，\frac{π}{4}}）$ | C． | $（{-\frac{3π}{4}，-\frac{π}{2}}）$ | D． | （$\frac{π}{2}$，π） |