题目内容
定义方程f(x)=f’(x)的实数根x0叫做函数f(x)的“新驻点”,如果函数g(x)=x,h(x)=ln(x+1),φ(x)=cosx(x∈0,π)的“新驻点”分别为α,β,γ,那么α,β,γ的大小关系是
- A.α<β<γ
- B.α<γ<β
- C.γ<α<β
- D.β<α<γ
D
解:根据题意可得:g′(x)=1,h′(x)="1" x+1 ,φ′(x)=-sinx,
所以α=1,ln(β+1)=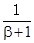 ,cosγ=-sinγ,
,cosγ=-sinγ,
①∵ln(β+1)=![]() ,,
,,
∴(β+1)β+1=e,
当β≥1时,β+1≥2,
∴β+1≤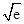 <2,
<2,
∴β<1,这与β≥1矛盾,
∴0<β<1;
②∵cosγ=-sinγ,γ∈( ,π),
,π),
∴γ=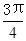 >1.
>1.
∴γ>α>β.
故选D.
解:根据题意可得:g′(x)=1,h′(x)="1" x+1 ,φ′(x)=-sinx,
所以α=1,ln(β+1)=
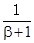 ,cosγ=-sinγ,
,cosγ=-sinγ,①∵ln(β+1)=
∴(β+1)β+1=e,
当β≥1时,β+1≥2,
∴β+1≤
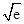 <2,
<2,∴β<1,这与β≥1矛盾,
∴0<β<1;
②∵cosγ=-sinγ,γ∈(
 ,π),
,π),∴γ=
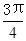 >1.
>1.∴γ>α>β.
故选D.

练习册系列答案
相关题目
