题目内容
(14分)已知函数  (a>0)
(a>0)
(1)判断并证明y= 在x∈(0,+∞)上的单调性;
在x∈(0,+∞)上的单调性;
(2)若存在 ,使
,使 ,则称
,则称 为函数
为函数 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值,并求出不动点
的值,并求出不动点 ;
;
(3)设 =
= ,若y=
,若y= 在(0,+∞)上有三个零点 , 求
在(0,+∞)上有三个零点 , 求 的取值范围.
的取值范围.
【答案】
解:(1)
任取 、
、 ∈(0,+∞)设
∈(0,+∞)设 >
>

∵ >
> >0
>0
∴ -
- >0,
>0,
 >0
>0
∴ ,函数y=
,函数y= 在x∈(0,+∞)上单调递增。
在x∈(0,+∞)上单调递增。
(2)解:令 ,则
,则 ,
,
令△=0得 (负值舍去)
(负值舍去)
将 代入
代入 得
得 =1
=1
(3)∵ =
=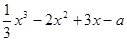 ,
,
∴  令
令 得x=1或x=3
得x=1或x=3
|
X |
(0,1) |
1 |
(1,3)[来源:Z|xx|k.Com] |
3 |
(3,+∞) |
|
|
+ |
0 |
- |
0 |
+ |
|
G(x) |
↑ |
|
↓ |
-a |
↑ |

【解析】略

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目

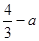
 (a∈R).
(a∈R). 时,
时,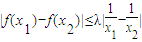 ,求λ的取值范围.
,求λ的取值范围. (a∈R).
(a∈R). 时,
时, ,求λ的取值范围.
,求λ的取值范围. ( a为常数、a∈R),
( a为常数、a∈R), .
. (a∈R).
(a∈R). 时,
时, ,求λ的取值范围.
,求λ的取值范围.