Question

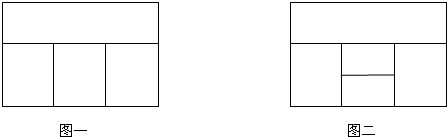
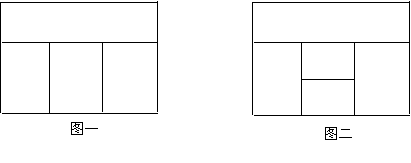
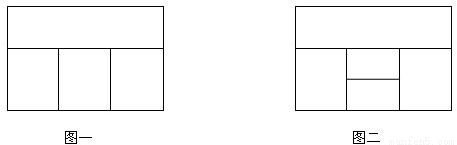
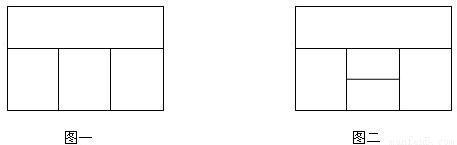
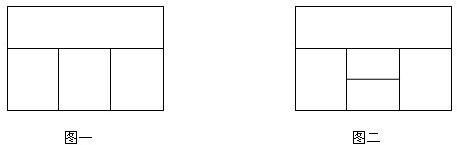
（1）用红、黄、蓝、白四种不同颜色的鲜花布置如图一所示的花圃，要求同一区域上用同一种颜色鲜花，相邻区域用不同颜色鲜花，问共有多少种不同的摆放方案？
（2）用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图二所示的花圃，要求同一区域上用同一种颜色鲜花，相邻区域使用不同颜色鲜花．求恰有两个区域用红色鲜花的概率；

Answer 1

分析：对于（1）根据分布计数原理依次摆放鲜花，可直接解得．
对于（2）求恰有两个区域用红色鲜花的概率．设M表示事件“恰有两个区域用红色鲜花”，把图二5个区域中的4个区域用A、B、D、E分别表示出来，然后分类讨论出①当区域A、D同色时和②当区域A、D不同色时的总的排列种数．再求出有两个区域同用红色的种数，相除即可得到答案．

解答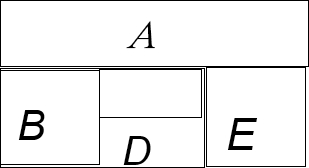：解：（1）根据分步计数原理，
摆放鲜花的不同方案有：4×3×2×2=48种．
（2）设M表示事件“恰有两个区域用红色鲜花”，
如下图，①当区域A、D同色时，共有5×4×3×1×3=180种；
②当区域A、D不同色时，共有5×4×3×2×2=240种；
因此，所有基本事件总数为：180+240=420种．
（由于只有A、D，B、E可能同色，故可按选用3色、4色、5色分类计算，求出基本事件总数为A₅³+2A₅⁴+A₅⁵=420种）
它们是等可能的．又因为A、D为红色时，共有4×3×3=36种；B、E为红色时，共有4×3×3=36种；
因此，事件M包含的基本事件有：36+36=72种．
所以，P（M）=

72

420

=

6

35

．

点评：此题主要考查分布乘法计数原理和简单的排列组合问题在实际中的应用，题中涉及到分类讨论思想，在高考中属于常用思想，同学们需要多加注意．