题目内容
已知直线l:(m+1)x-my+2m-
=0与圆C:x2+y2=2相切,且满足上述条件的直线l共有n条,则n的值为( )
| 2 |
| A.0 | B.1 |
| C.2 | D.以上答案都不对 |
由圆C的方程x2+y2=2,得到圆心C坐标(0,0),半径r=
,
∵直线l与圆C相切,
∴圆心C到直线(m+1)x-my+2m-
=0的距离d=r,
即
=
,解得m=
,
∴此时直线l的方程为x=
,
则满足上述条件的直线l共有1条,即n的值为1.
故选B
| 2 |
∵直线l与圆C相切,
∴圆心C到直线(m+1)x-my+2m-
| 2 |
即
|2m-
| ||
|
| 2 |
| 2 |
∴此时直线l的方程为x=
| 2 |
则满足上述条件的直线l共有1条,即n的值为1.
故选B

练习册系列答案
相关题目
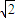 =0与圆C:x2+y2=2相切,且满足上述条件的直线l共有n条,则n的值为( )
=0与圆C:x2+y2=2相切,且满足上述条件的直线l共有n条,则n的值为( )