题目内容
设a>0且a≠1,f(x)=-x2+ax,对x∈(-| 1 |
| 2 |
| 1 |
| 2 |
分析:据题意列出恒成立的不等式,结合指数函数与二次函数的图象写出不等式恒成立的充要条件,解不等式得解.
解答:解:f(x)>0即ax>x2在(-
,
)恒成立
∴
解得
∵a>0且a≠1
故答案为[
,1)∪(1,16]
| 1 |
| 2 |
| 1 |
| 2 |
∴
|
解得
|
∵a>0且a≠1
故答案为[
| 1 |
| 16 |
点评:本题考查利用基本初等函数的图象解决不等式恒成立问题.

练习册系列答案
相关题目
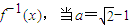 时,比较f-1[g(x)]与-1的大小,证明你的结论;
时,比较f-1[g(x)]与-1的大小,证明你的结论;