题目内容
已知焦点(设为F1,F2)在x轴上的双曲线上有一点P(x0,
),直线y=
x线的一条渐近线,当
•
=0,双曲线的一个顶点坐标是( )
| 3 |
| 2 |
| 3 |
| FP1 |
| PF2 |
A.(
| B.(
| C.(2,0) | D.(1,0) |
∵双曲线在x轴上,直线y=
x是渐近线
∴
=
即b2=3a2
设双曲线方程为
-
=1 F1(-C,0)F2(C,0)
把P(x0,
)代入方程整理得x02=
∵
•
=0∴PF1⊥PF2
∴|PF1|2+|PF2|2=|F1F2|2 即(x0+c)2+
+(x0-c)2+
=4c2
整理得a2-c2=-6
∵c2=a2+b2=4a2
∴-3a2=-6
∴a=
故选A.
| 3 |
∴
| b |
| a |
| 3 |
设双曲线方程为
| x2 |
| a2 |
| y2 |
| 3a2 |
把P(x0,
| 3 |
| 2 |
| 4a2-3 |
| 4 |
∵
| FP1 |
| PF2 |
∴|PF1|2+|PF2|2=|F1F2|2 即(x0+c)2+
| 9 |
| 4 |
| 9 |
| 4 |
整理得a2-c2=-6
∵c2=a2+b2=4a2
∴-3a2=-6
∴a=
| 2 |
故选A.

练习册系列答案
相关题目
已知焦点(设为F1,F2)在x轴上的双曲线上有一点P(x0,
),直线y=
x线的一条渐近线,当
•
=0,双曲线的一个顶点坐标是( )
| 3 |
| 2 |
| 3 |
| FP1 |
| PF2 |
A、(
| ||
B、(
| ||
| C、(2,0) | ||
| D、(1,0) |
已知焦点(设为F1,F2)在x轴上的双曲线上有一点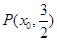 ,直线
,直线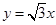 是双曲线的一条渐近线,当
是双曲线的一条渐近线,当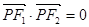 时,该双曲线的一个顶点坐标是
时,该双曲线的一个顶点坐标是
A.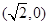 | B.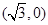 | C.(2,0) | D.(1,0) |
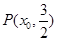 ,直线
,直线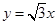 是双曲线的一条渐近线,当
是双曲线的一条渐近线,当 时,该双曲线的一个顶点坐标是 ( )
时,该双曲线的一个顶点坐标是 ( )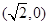 B.
B.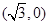 C.(2,0) D.(1,0)
C.(2,0) D.(1,0)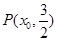 ,直线
,直线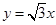 是双曲线的一条渐近线,当
是双曲线的一条渐近线,当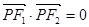 时,该双曲线的一个顶点坐标是
时,该双曲线的一个顶点坐标是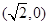 B.
B.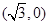 C.(2,0) D.(1,0)
C.(2,0) D.(1,0) ,直线
,直线 是双曲线的一条渐近线,当
是双曲线的一条渐近线,当 时,该双曲线的一个顶点坐标是
时,该双曲线的一个顶点坐标是 B.
B. C.(2,0) D.(1,0)
C.(2,0) D.(1,0)