题目内容

已知函数f(x)是定义在R上的偶函数,且对任意的x∈R,都有f(x+2)=f(x).当0≤x≤1时,f(x)=x2.若直线y=x+a与函数y=f(x)的图象在[0,2]内恰有两个不同的公共点,则实数a的值是(　　)

(A)0 (B)0或-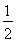

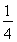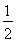(C)-或- (D)0或-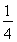

 

【答案】

D

【解析】∵f(x+2)=f(x),

∴T=2.

又0≤x≤1时,f(x)=x2,可画出函数y=f(x)在一个周期内的图象如图所示.

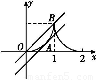
显然a=0时,y=x与y=x2在[0,2]内恰有两个不同的公共点.

另当直线y=x+a与y=x2(0≤x≤1)相切时也恰有两个不同公共点,

由题意知y'=(x2)'=2x=1,

∴x=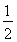.∴A,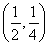

又A点在y=x+a上,

∴a=-.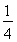

综上知选D.

 

练习册系列答案
相关题目
已知函数f(x)=
1
3
x3+
a-3
2
x2+(a2-3a)x-2a．
（I）如果对任意x∈[1，2]，f′（x）＞a2恒成立，求实数a的取值范围；
（II）设函数f（x）的两个极值点分别为x1，x2判断下列三个代数式：①x1+x2+a，②
x
2
1
+
x
2
2
+a2，③
x
3
1
+
x
3
2
+a3
中有几个为定值？并且是定值请求出；若不是定值，请把不是定值的表示为函数g（a），并求出g（a）的最小值．
问题1：已知函数f(x)=
x
1+x
，则f(
1
10
)+f(
1
9
)+…+f(
1
2
)+f(1)+f(2)+…+f（9）+f（10）=
19
2
19
2
．
我们若把每一个函数值计算出，再求和，对函数值个数较少时是常用方法，但函数值个数较多时，运算就较繁锁．观察和式，我们发现f(
1
2
)+f(2)、…、f(
1
9
)+f(9)、f(
1
10
)+f(10)可一般表示为f(
1
x
)+f(x)=
1
x
1+
1
x
+
x
1+x
=
1
1+x
+
x
1+x
=
1+x
1+x
=1为定值，有此规律从而很方便求和，请求出上述结果，并用此方法求解下面问题：
问题2：已知函数f(x)=
1
2x+
2
，求f（-2007）+f（-2006）+…+f（-1）+f（0）+f（1）+…+f（2007）+f（2008）的值．
已知函数f(x)=
x+1-a
a-x
(x≠a)
（1）当f（x）的定义域为[a+
1
2
，a+1]时，求f（x）的值域；
（2）试问对定义域内的任意x，f（2a-x）+f（x）的值是否为一个定值？若是，求出这个定值；若不是，说明理由；
（3）设函数g（x）=x2+|（x-a）f（x）|，若
1
2
≤a≤
3
2
，求g（x）的最小值．
已知函数f(x)=log3
3
x
1-x
，M(x1，y1)，N(x2，y2)是f（x）图象上的两点，横坐标为
1
2
的点P满足2
OP
=
OM
+
ON
（O为坐标原点）．
（1）求证：y1+y2为定值；
（2）若Sn=f(
1
n
)+f(
2
n
)+…+f(
n-1
n
)，其中n∈N*，n≥2令an=
1
6
，n=1
1
4(Sn+1)(Sn+1+1)
，n≥2
，其中n∈N*，Tn为数列{an}的前n项和，若Tn＜m（Sn+1+1）对一切n∈N*都成立，试求m的取值范围．
（3）对于给定的实数a（a＞1）是否存在这样的数列{an}，使得f(an)=log3(
3
an+1)，且a1=
1
a-1
？若存在，求出a满足的条件；若不存在，请说明理由．
（2009•嘉定区一模）（理）已知函数f(x)=log2
2
x
1-x
，P1（x1，y1）、P2（x2，y2）是f（x）图象上两点．
（1）若x1+x2=1，求证：y1+y2为定值；
（2）设Tn=f(
1
n
)+f(
2
n
)+…+f(
n-1
n
)，其中n∈N*且n≥2，求Tn关于n的解析式；
（3）对（2）中的Tn，设数列{an}满足a1=2，当n≥2时，an=4Tn+2，问是否存在角a，使不等式(1-
1
a1
)(1-
1
a2
)…(1-
1
an
)＜
sinα
2n+1
对一切n∈N*都成立？若存在，求出角α的取值范围；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网