题目内容
已知y=f(x)是函数y=
(a≠0,a∈R)的反函数,g(x)=
(Ⅰ)解关于x的不等式:1+ef(x)+g(x)>0;
(Ⅱ)当a=1时,过点(1,-1)是否存在函数y=f(x)图象的切线?若存在,有多少条?若不存在,说明理由;
(Ⅲ)若a是使f(x)≥g(x)(x≥1)恒成立的最小值,试比较
与f[(1+n)λ2n(1-λ)]的大小(0<λ<1,n∈N*).
| ex |
| a |
| x-1 |
| x |
(Ⅰ)解关于x的不等式:1+ef(x)+g(x)>0;
(Ⅱ)当a=1时,过点(1,-1)是否存在函数y=f(x)图象的切线?若存在,有多少条?若不存在,说明理由;
(Ⅲ)若a是使f(x)≥g(x)(x≥1)恒成立的最小值,试比较
| n |
 |
| k=1 |
| 1 |
| 1+kλ |
分析:(I)先求出函数y=
(a≠0,a∈R)的反函数f(x),把f(x)代入化简后,再对a进行分类讨论,转化为一元二次不等式,则不等式易解;
(Ⅱ)设出切点,用导数工具刻画出函数的单调性和关键点,进而得出切线的情况;
(Ⅲ)把恒成立问题转化为函数的最值来求解a值,再利用
≤(
)λ,即1+kλ≤21-λ(1+k)λ,来进行证明即可.
| ex |
| a |
(Ⅱ)设出切点,用导数工具刻画出函数的单调性和关键点,进而得出切线的情况;
(Ⅲ)把恒成立问题转化为函数的最值来求解a值,再利用
| 1+kλ |
| 2 |
| 1+k |
| 2 |
解答:解:(1)由已知可得f(x)=lnax,当a>0时,f(x)的定义域为(0,+∞);
当a<0时,f(x)的定义域为(-∞,0)
①当a>0时,x>0,原不等式等价于:1+ax+
>0?ax2+2x-1>0,
可得 x∈(
,+∞);
②当a<0时,x<0,原不等式等价于:1+ax+
<0?ax2+2x-1<0,
可得 x∈(-∞,0). (4分)
(2)设y=f(x)图象上的切点坐标为(x0,f(x0)),显然x0≠1,
可得f′(x0)=
=
⇒lnx0=-
,
设h(x0)=lnx0+
(x0>0,x0≠1),h′(x0)=
,
可得h(x0)在(1,+∞)为增区间;(0,1)为减区间,h(x0)>h(1)=1
所以h(x0)=0没有实根,故不存在切线.(9分)
(3)∵lnax≥
对x≥1恒成立,所以lna+lnx≥
⇒lna≥1-
-lnx,
令h(x)=1-
-lnx,h′(x)=
-
≤0(x≥1),可得h(x)在区间[1,+∞)上单调递减,
故lna≥h(1)=0,amin=1.得lnx≥
(x≥1),f(x)=lnx.
令x=
(k∈N*),ln(1+kλ)-lnkλ>
,
而
≤(
)λ,即1+kλ≤21-λ(1+k)λ,
所以
<ln(1+kλ)-lnkλ≤ln(1+k)λ-lnkλ+ln21-λ,
<ln(1+n)λ+nln21-λ=f[(1+n)λ2n(1-λ)]. (14分)
当a<0时,f(x)的定义域为(-∞,0)
①当a>0时,x>0,原不等式等价于:1+ax+
| x-1 |
| x |
可得 x∈(
| ||
| a |
②当a<0时,x<0,原不等式等价于:1+ax+
| x-1 |
| x |
可得 x∈(-∞,0). (4分)
(2)设y=f(x)图象上的切点坐标为(x0,f(x0)),显然x0≠1,
可得f′(x0)=
| 1 |
| x0 |
| lnx0 |
| x0-1 |
| 1 |
| x0 |
设h(x0)=lnx0+
| 1 |
| x0 |
| x0-1 |
| x0 |
可得h(x0)在(1,+∞)为增区间;(0,1)为减区间,h(x0)>h(1)=1
所以h(x0)=0没有实根,故不存在切线.(9分)
(3)∵lnax≥
| x-1 |
| x |
| x-1 |
| x |
| 1 |
| x |
令h(x)=1-
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
故lna≥h(1)=0,amin=1.得lnx≥
| x-1 |
| x |
令x=
| 1+kλ |
| kλ |
| 1 |
| 1+kλ |
而
| 1+kλ |
| 2 |
| 1+k |
| 2 |
所以
| 1 |
| 1+kλ |
| n |
 |
| k=1 |
| 1 |
| 1+kλ |
点评:本题为函数与导数的综合,涉及不等式的解法和函数恒成立问题以及切线问题,属中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
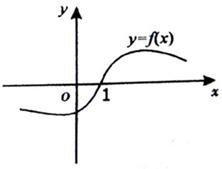 已知函数f(x)(x∈R)的一段图象如图所示,f′(x)是函f(x)(数的导函数,且y=f(x+1)是奇函数,给出以下结论:
已知函数f(x)(x∈R)的一段图象如图所示,f′(x)是函f(x)(数的导函数,且y=f(x+1)是奇函数,给出以下结论: 已知函数f(x)=
已知函数f(x)=