题目内容
设某大学的女生体重 (单位:kg)与身高
(单位:kg)与身高 (单位:cm) 具有线性相关关系,根据一组样本数据(
(单位:cm) 具有线性相关关系,根据一组样本数据( ,
, )(i=1,2,…,n),用最小二乘法建立的回归方程为
)(i=1,2,…,n),用最小二乘法建立的回归方程为 =0.85x-85.71,则下列结论中不正确的是 ( )
=0.85x-85.71,则下列结论中不正确的是 ( )
A. 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心( , , ) ) |
| C.若该大学某女生身高为170cm,则可断定其体重必为58.79kg |
| D.若该大学某女生身高增加1cm,则其体重约增加0.85kg |
C
解析试题分析:解:对于A,0.85>0,所以y与x具有正的线性相关关系,故正确;对于B,回归直线过样本点的中心( ,
, ),故正确;对于D,∵回归方程为
),故正确;对于D,∵回归方程为 =0.85x-85.71,∴该大学某女生身高增加1cm,则其体重约增加0.85kg,故正确;对于C,x=170cm时,
=0.85x-85.71,∴该大学某女生身高增加1cm,则其体重约增加0.85kg,故正确;对于C,x=170cm时, =0.85×170-85.71=58.79,但这是预测值,不可断定其体重为58.79kg,故不正确,故选C
=0.85×170-85.71=58.79,但这是预测值,不可断定其体重为58.79kg,故不正确,故选C
考点:线性回归方程
点评:本题考查线性回归方程,考查学生对线性回归方程的理解,属于中档题.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.每组命中个数的茎叶图如下.则下面结论中错误的一个是( )
| A.甲的极差是29 |
| B.乙的众数是21 |
| C.甲罚球命中率比乙高 |
| D.甲的中位数是24 |
某班学生在一次数学考试中成绩分布如下表:
| 分数段 | [0,60) | [60,70) | [70,80) | [80,90) |
| 人数 | 6 | 5 | 6 | 8 |
| 分数段 | [90,100) | [100,110) | [110,120) | [120,150) |
| 人数 | 10 | 6 | 4 | 5 |
A.0.18 B.0.40 C.0.50 D.0.38
甲乙两位同学在高三的5次月考中数学成绩统计如茎叶图所示,若甲乙两人的平均成绩分别是 ,则下列正确的是( )
,则下列正确的是( )
A. ;乙比甲成绩稳定 ;乙比甲成绩稳定 |
B. ;甲比乙成绩稳定 ;甲比乙成绩稳定 |
C. ;乙比甲成绩稳定 ;乙比甲成绩稳定 |
D. ;甲比乙成绩稳定 ;甲比乙成绩稳定 |
某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是( )
| A.y=-10x+200 | B.y=10x+200 |
| C.y=-10x-200 | D.y=10x-200 |
在样本的频率分布直方图中,共有11个小长方体,若中间一个小长方体的面积等于其他10个小长方体的面积和的 ,且样本容量为160,则中间一组频数为( )
,且样本容量为160,则中间一组频数为( )
| A.32 | B.0.2 | C.40 | D.0.25 |
某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该种日用品中随机抽取200件,对其等级系数进行统计分析,得到频率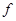 的分布表如下:
的分布表如下:
则在所取的200件日用品中,等级系数X=1的件数为
| A.40 | B.20 | C.30 | D.60 |
已知某单位有职工120人,其中男职工90人。现在采用分层抽样(按男女分层)抽取一个样本,若样本中有3名女职工,则样本容量为( )。
| A.9 | B.12 | C.10 | D.15 |
 )负相关,则其回归方程可能是( )
)负相关,则其回归方程可能是( ) B.
B. C.
C.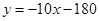 D
D 