题目内容
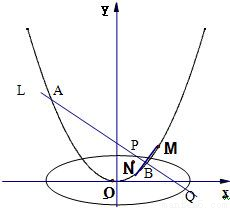
如图,已知M(m,m2)、N(n,n2)是抛物线C:y=x2上两个不同点,且m2+n2=1,m+n≠0,直线l是线段MN的垂直平分线.设椭圆E的方程为 .
.(Ⅰ)当M、N在抛物线C上移动时,求直线L斜率k的取值范围;
(Ⅱ)已知直线L与抛物线C交于A、B、两个不同点,L与椭圆E交于P、Q两个不同点,设AB中点为R,OP中点为S,若
 ,求椭圆E离心率的范围.
,求椭圆E离心率的范围.
【答案】分析:(1)先用M,N的坐标表示出直线MN的斜率,进而表示出直线l的斜率,根据m2+n2=1,由m2+n2≥2mn求得m和n的不等式关系,进而求得k的范围.
(2)先根据题意整理出直线l的方程,进而代入椭圆和抛物线方程,利用P,S表示出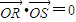 求得a和k的关系,利用(1)中k的范围求得a的范围,进而求得椭圆离心率的范围.
求得a和k的关系,利用(1)中k的范围求得a的范围,进而求得椭圆离心率的范围.
解答:解:(1)∵直线MN的斜率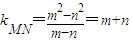 ,
,
又∵l⊥MN,m+n≠0,∴直线l的斜率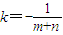
∵m2+n2=1,由m2+n2≥2mn,得2(m2+n2)≥(m+n)2,
即2≥(m+n)2,∴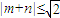
因M、N两点不同,∴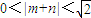 ,
,
∴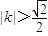
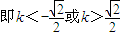
(2)∵l方程为: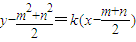 ,
,
又∵m2+n2=1,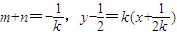 ,
,
∴l:y=kx+1,代入抛物线和椭圆方程并整理得:x2-kx-1=0(1),
(a+2k2)x2+4kx+2-2a=0(2)
易知方程(1)的判别式△1=k2+4>0恒成立,方程(2)的判别式△2=8a(2k2+a-1)
∵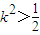 ,a>0,
,a>0,
∴2k2+a-1>a>0,∴△2>0恒成立
∵R(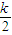 ,
,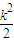 +1),S(
+1),S(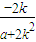 ,
,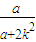 ),
),
由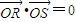 得:
得: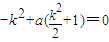 ,
,
∴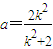 ,
,
∵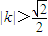 ,∴a=
,∴a=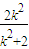 =2-
=2-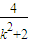 >2-
>2- =
=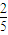 ,
,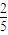 <a<2,
<a<2,
∴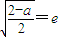 ,∴a=2-2e2>
,∴a=2-2e2>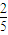 ,
,
e2<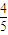 ,∴0<e<
,∴0<e<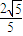 ,
,
∴椭圆E离心率的取值范围是(0,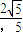 )
)
点评:本题主要考查了直线与圆锥曲线的综合问题.常涉及到圆锥曲线的性质和直线的基本知识点,如直线被圆锥曲线截得的弦长、弦中点问题,垂直问题,对称问题.与圆锥曲线性质有关的量的取值范围等是近几年命题的新趋向.
(2)先根据题意整理出直线l的方程,进而代入椭圆和抛物线方程,利用P,S表示出
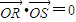 求得a和k的关系,利用(1)中k的范围求得a的范围,进而求得椭圆离心率的范围.
求得a和k的关系,利用(1)中k的范围求得a的范围,进而求得椭圆离心率的范围.解答:解:(1)∵直线MN的斜率
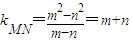 ,
,又∵l⊥MN,m+n≠0,∴直线l的斜率
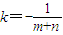
∵m2+n2=1,由m2+n2≥2mn,得2(m2+n2)≥(m+n)2,
即2≥(m+n)2,∴
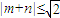
因M、N两点不同,∴
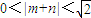 ,
,∴
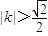
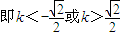

(2)∵l方程为:
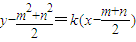 ,
,又∵m2+n2=1,
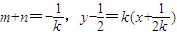 ,
,∴l:y=kx+1,代入抛物线和椭圆方程并整理得:x2-kx-1=0(1),
(a+2k2)x2+4kx+2-2a=0(2)
易知方程(1)的判别式△1=k2+4>0恒成立,方程(2)的判别式△2=8a(2k2+a-1)
∵
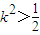 ,a>0,
,a>0,∴2k2+a-1>a>0,∴△2>0恒成立
∵R(
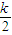 ,
,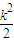 +1),S(
+1),S(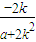 ,
,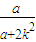 ),
),由
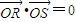 得:
得: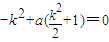 ,
,∴
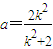 ,
,∵
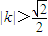 ,∴a=
,∴a=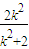 =2-
=2-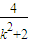 >2-
>2- =
=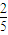 ,
,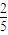 <a<2,
<a<2,∴
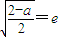 ,∴a=2-2e2>
,∴a=2-2e2>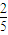 ,
,e2<
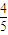 ,∴0<e<
,∴0<e<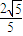 ,
,∴椭圆E离心率的取值范围是(0,
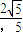 )
)点评:本题主要考查了直线与圆锥曲线的综合问题.常涉及到圆锥曲线的性质和直线的基本知识点,如直线被圆锥曲线截得的弦长、弦中点问题,垂直问题,对称问题.与圆锥曲线性质有关的量的取值范围等是近几年命题的新趋向.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目






 .
. ,求椭圆E离心率的范围.
,求椭圆E离心率的范围.