题目内容
(2010•重庆一模)设集合A={(x,y)|x2+y2≤1},集合B={(x,y)|log|x||y|≤log|y||x|,|x|<1,|y|<1},则在直角坐标平面内,A∩B所表示的平面区域的面积为( )
分析:集合A={(x,y)|x2+y2≤1},集合B={(x,y)|log|x||y|≤log|y||x|,|x|<1,|y|<1}={(x,y)||x|<|y|},在平面中作出A和B的图象,由此能求出A∩B所表示的平面区域的面积.
解答: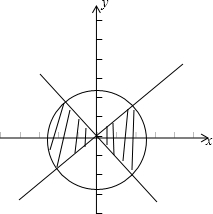 解:∵集合A={(x,y)|x2+y2≤1},
解:∵集合A={(x,y)|x2+y2≤1},
集合B={(x,y)|log|x||y|≤log|y||x|,|x|<1,|y|<1}={(x,y)||x|<|y|},,
在平面中作出A和B的图象,
结合图象,知A∩B所表示的平面区域的面积为圆x2+y2=1的面积的一半,即
.
故选D.
 解:∵集合A={(x,y)|x2+y2≤1},
解:∵集合A={(x,y)|x2+y2≤1},集合B={(x,y)|log|x||y|≤log|y||x|,|x|<1,|y|<1}={(x,y)||x|<|y|},,
在平面中作出A和B的图象,
结合图象,知A∩B所表示的平面区域的面积为圆x2+y2=1的面积的一半,即
| π |
| 2 |
故选D.
点评:本题考查交集及其运算,解题时要认真审题,仔细解答,注意数形结合的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目