题目内容
设 是等差数列,若
是等差数列,若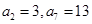 ,则数列
,则数列 前8项的和为( )
前8项的和为( )
| A.128 | B.80 | C.64 | D.56 |
C.
解析试题分析: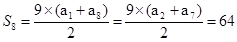 。
。
考点:本题考查等差数列的性质和前n项和公式。
点评:在等差数列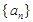 中,
中,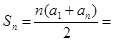
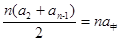 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
等差数列{an}的通项公式为an=2n+1,其前n项和为Sn,则{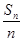 }前10项和为
}前10项和为
| A.120 | B.100 | C.75 | D.70 |
在数列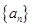 中,
中, ,
,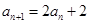 ,则
,则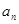 等于( )
等于( )
A.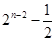 | B.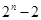 | C.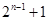 | D.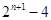 |
已知递增等差数列 中,
中,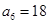 且
且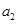 是
是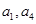 的等比中项,则它的第4项到第11项的和为
的等比中项,则它的第4项到第11项的和为
| A.180 | B.198 | C.189 | D.168 |
已知等差数列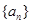 中,前
中,前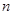 项和
项和 ,且
,且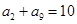 ,则
,则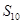 等于( )
等于( )
A.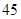 | B.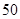 | C.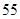 | D.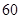 |
已知等差数列{an}的前n项和为Sn,S9=-36,S13=-104,等比数列{bn}中,b5=a5,b7=a7,则b6的值为
A.±4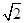 | B.-4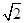 | C.4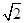 | D.无法确定 |
已知等差数列 的公差为
的公差为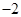 ,且
,且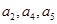 成等比数列,则
成等比数列,则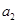 等于 ( )
等于 ( )
| A.-4 | B.-6 | C.-8 | D.8 |
已知数列 是等差数列,且
是等差数列,且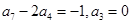 ,则公差
,则公差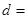
| A.-2 | B.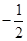 | C.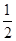 | D.2 |
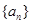 的前
的前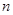 项和为
项和为 ,关于数列
,关于数列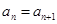 ;
;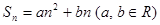 ,则数列
,则数列 ,则数列
,则数列