题目内容
求函数
的最大值．
【答案】分析：由函数的解析式先求其定义域，然后利用三角换元和二倍角的余弦公式，将次问题转化为三角函数的最值问题，即可得解．
解答：解：∵
∴
∴-2≤x≤2∴令x=2cos2t，2t∈[0，2π]∴t∈[0，π]
∴
=
=3×2sint+4×2|cost|=6sint±8cost
=10sin（t±φ） 其中tanφ=
∴
的最大值为10．
点评：本题通过三角换元将函数F（x）转化为三角函数，主要考查了二倍角的余弦公式及两角和与差的正弦公式，在换元的时候注意变量的范围．
解答：解：∵
∴
∴-2≤x≤2∴令x=2cos2t，2t∈[0，2π]∴t∈[0，π]∴
==3×2sint+4×2|cost|=6sint±8cost=10sin（t±φ） 其中tanφ=
∴
的最大值为10．点评：本题通过三角换元将函数F（x）转化为三角函数，主要考查了二倍角的余弦公式及两角和与差的正弦公式，在换元的时候注意变量的范围．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
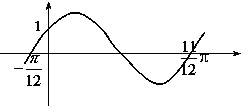已知函数y=2sin（ωx+?）（ω＞0，|?|＜