题目内容
已知函数f（x）
，则方程f（2x2+x）=a（a＞2）的根的个数可能为______（将正确命题的序号全部填入）
①1个②2个③3个④4个⑤5个⑥6个．
|
①1个②2个③3个④4个⑤5个⑥6个．
画出函数f（x）=
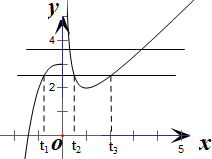
的图象如右图，
令t=2x2+x，
当2＜a≤3时，y=a与y=f（t）的图象有三个交点，三个交点的横坐标记为t1，t2，t3且t1≤0＜t2＜t3，
当2x2+x=t2时，该方程有两解，2x2+x=t3时，该方程也有两解，2x2+x=t1时，该方程有0个解或1个解或2个解，
∴当2＜a≤3时，方程f（2x2+x）=a的根的个数可能为4个，5个，6个；
当a＞3时，y=a与y=f（t）的图象有两个交点，两个交点的横坐标记为t4，t5且0＜t4＜t5，
当2x2+x=t4时，该方程有两解，2x2+x=t5时，该方程也有两解，
∴当a＞3时，方程f（2x2+x）=a的根的个数为4个；
综上所述：方程f（2x2+x）=a（a＞2）的根的个数可能为4个，5个，6个．
故答案为：④⑤⑥．
|
令t=2x2+x，
当2＜a≤3时，y=a与y=f（t）的图象有三个交点，三个交点的横坐标记为t1，t2，t3且t1≤0＜t2＜t3，
当2x2+x=t2时，该方程有两解，2x2+x=t3时，该方程也有两解，2x2+x=t1时，该方程有0个解或1个解或2个解，
∴当2＜a≤3时，方程f（2x2+x）=a的根的个数可能为4个，5个，6个；
当a＞3时，y=a与y=f（t）的图象有两个交点，两个交点的横坐标记为t4，t5且0＜t4＜t5，
当2x2+x=t4时，该方程有两解，2x2+x=t5时，该方程也有两解，
∴当a＞3时，方程f（2x2+x）=a的根的个数为4个；
综上所述：方程f（2x2+x）=a（a＞2）的根的个数可能为4个，5个，6个．
故答案为：④⑤⑥．
练习册系列答案
相关题目
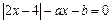恰有两个不相等实根的充要条件是 ．