题目内容
“m=-4”是“直线mx+8y-2=0与直线2x+my-1=0平行”的（ ）
分析：结合直线平行的等价条件，利用充分条件和必要条件的定义进行判断．
解答：解：若m=-4，则两直线方程分别为-4x+8y-2=0，和2x-4y-1=0，即2x-4y+1=0和2x-4y-1=0，满足直线平行．
若直线mx+8y-2=0与直线2x+my-1=0平行，则由
=
≠
，解得m2=16，且m≠4．所以m=-4．
所以“m=-4”是“直线mx+8y-2=0与直线2x+my-1=0平行”充要条件．
故选C．
若直线mx+8y-2=0与直线2x+my-1=0平行，则由
| 2 |
| m |
| m |
| 8 |
| -1 |
| -2 |
所以“m=-4”是“直线mx+8y-2=0与直线2x+my-1=0平行”充要条件．
故选C．
点评：本题主要考查直线与直线平行的充要条件的判断，要求熟练掌握直线平行的等价条件．
练习册系列答案
名校课堂系列答案
相关题目
下列说法正确的是（ ）
A、若a＞b，则
| ||||||
| B、函数f（x）=ex-2的零点落在区间（0，1）内 | ||||||
C、函数f（x）=
| ||||||
| D、“m=4”是“直线2x+my+1=0与直线mx+8y+2=0互相平行”的充分条件 |
)x+(m+2)y+3=0相互平行”的
)x+(m+2)y+3=0相互平行”的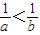 
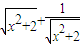的最小值为2