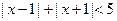题目内容
(本小题满分10分)选修4-5:不等式选讲
关于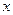 的不等式
的不等式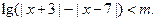
(Ⅰ)当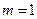 时,解不等式;
时,解不等式;
(Ⅱ)设函数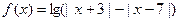 ,当
,当 为何值时,
为何值时,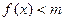 恒成立?
恒成立?
关于
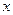 的不等式
的不等式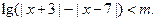
(Ⅰ)当
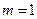 时,解不等式;
时,解不等式;(Ⅱ)设函数
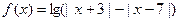 ,当
,当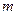 为何值时,
为何值时,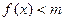 恒成立?
恒成立?(Ⅰ)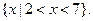
(Ⅱ)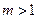
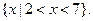
(Ⅱ)
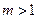
(Ⅰ)当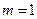 时,
时, 原不等式可变为
原不等式可变为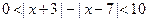 ,
,
可得其解集为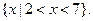
(Ⅱ)设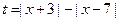 ,
,
则由对数定义及绝对值的几何意义知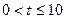 ,
,
因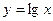 在
在 上为增函数,
上为增函数,
则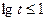 ,当
,当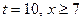 时,
时,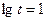 ,
,
故只需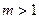 即可,
即可,
即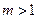 时,
时,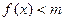 恒成
恒成
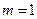 时,
时, 原不等式可变为
原不等式可变为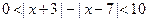 ,
,可得其解集为
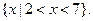
(Ⅱ)设
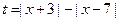 ,
,则由对数定义及绝对值的几何意义知
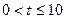 ,
,因
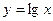 在
在 上为增函数,
上为增函数,则
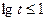 ,当
,当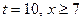 时,
时,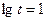 ,
,故只需
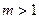 即可,
即可,即
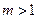 时,
时,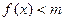 恒成
恒成
练习册系列答案
相关题目
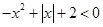 的解集是
的解集是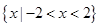
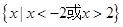
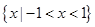
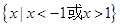
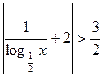 的解集为 .
的解集为 .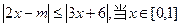 时恒成立,则实数m的取值范围为 。
时恒成立,则实数m的取值范围为 。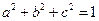 ,若
,若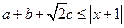 对任意实数a,b,c恒成立,求实数
对任意实数a,b,c恒成立,求实数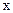 的取值范围。
的取值范围。 的解集是
的解集是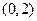
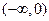
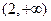

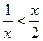 。
。