题目内容
已知等差数列{an}的首项a1=16,公差d=-
,当|an|最小时的n值为 .
| 3 |
| 4 |
考点:等差数列的通项公式
专题:
分析:由题意可得通项公式,可得前22项均为正数,从第23项开始为负,求a22和a23,比较绝对值可得.
解答:
解:∵等差数列{an}的首项a1=16,公差d=-
,
∴通项公式an=16-
(n-1)=
(67-3n),
令an=
(67-3n)≤0可得n≥
,
∴等差数列{an}的前22项均为正数,从第23项开始为负,
又a22=
,a23=-
,∴当|an|最小时的n值为22
故答案为:22
| 3 |
| 4 |
∴通项公式an=16-
| 3 |
| 4 |
| 1 |
| 4 |
令an=
| 1 |
| 4 |
| 67 |
| 3 |
∴等差数列{an}的前22项均为正数,从第23项开始为负,
又a22=
| 1 |
| 4 |
| 1 |
| 2 |
故答案为:22
点评:本题考查等差数列的通项公式,属基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知正方形OABC的四个顶点分别是0(0,0),A(1,0),B(1,1),C(0,1)设u=x2-y2,v=2xy是一个由平面xOy到平面uOv上的变换,则正方形OABC在这个变换下的图形是( )
A、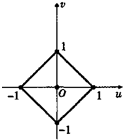 |
B、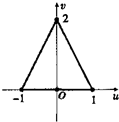 |
C、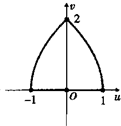 |
D、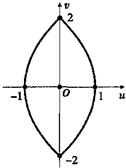 |
已知点P(sinα-cosα,2)在第二象限,则α的一个变化区间是( )
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(
|
设{an}是等差数列,若a5=log
8,则a4+a6等于( )
2 |
| A、6 | B、8 | C、9 | D、16 |