题目内容
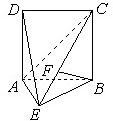 如图,DA⊥平面ABE,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,DA⊥平面ABE,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.(Ⅰ)求证:AE⊥平面BCE;
(Ⅱ)求二面角B-AC-E的平面角的正切值.
分析:(Ⅰ)要证AE⊥平面BCE,只需证明AE垂直平面BCE内的两条相交直线BC和BF,即可.
(Ⅱ)连接BD交AC于点O,连接OF,由三垂线定理的逆定理,得FO⊥AC,∠BOF是二面角B-AC-E的平面角,然后求二面角B-AC-E的平面角的正切值.
(Ⅱ)连接BD交AC于点O,连接OF,由三垂线定理的逆定理,得FO⊥AC,∠BOF是二面角B-AC-E的平面角,然后求二面角B-AC-E的平面角的正切值.
解答::解(Ⅰ)证明:∵BF⊥平面ACE,∴BF⊥AE.(1分)
∵DA⊥平面ABE,∴DA⊥AE.(2分)
∵四边形ABCD是正方形,
∴BC∥AD,∴BC⊥AE.(4分)
∵BC∩BF=B,∴AE⊥平面BCE.(5分)
(Ⅱ)解:连接BD交AC于点O,连接OF.
∵正方形ABCD的边长为2,
∴BO⊥AC,且BO=
.(6分)
∵BF⊥平面ACE,
∴由三垂线定理的逆定理,得FO⊥AC.(7分)
∴∠BOF是二面角B-AC-E的平面角.(8分)
由(Ⅰ)知AE⊥平面BCE,∴AE⊥BE.
又∵AE=EB,
∴在等腰直角三角形AEB中,AE=BE=
.
在直角△BCE中,EC=
=
,(9分)
∵BF⊥平面ACE,EC?平面ACE,OF?平面ACE
∴BF⊥EC,BF⊥OF.(10分)
∴BF=
=
.(11分)
在直角△BOF中,OF=
=
.(12分)
∴tan∠BOF=
=
=
.
∴二面角B-AC-E的平面角的正切值为
.(13分)
∵DA⊥平面ABE,∴DA⊥AE.(2分)
∵四边形ABCD是正方形,
∴BC∥AD,∴BC⊥AE.(4分)
∵BC∩BF=B,∴AE⊥平面BCE.(5分)
(Ⅱ)解:连接BD交AC于点O,连接OF.
∵正方形ABCD的边长为2,
∴BO⊥AC,且BO=
| 2 |
∵BF⊥平面ACE,
∴由三垂线定理的逆定理,得FO⊥AC.(7分)
∴∠BOF是二面角B-AC-E的平面角.(8分)
由(Ⅰ)知AE⊥平面BCE,∴AE⊥BE.
又∵AE=EB,
∴在等腰直角三角形AEB中,AE=BE=
| 2 |
在直角△BCE中,EC=
| BC2+BE2 |
| 6 |
∵BF⊥平面ACE,EC?平面ACE,OF?平面ACE
∴BF⊥EC,BF⊥OF.(10分)
∴BF=
| BC•BE |
| EC |
2
| ||
| 3 |
在直角△BOF中,OF=
| BO2-BF2 |
| ||
| 3 |
∴tan∠BOF=
| BF |
| OF |
| ||||
|
| 2 |
∴二面角B-AC-E的平面角的正切值为
| 2 |
点评:本题考查直线与平面垂直的判定,二面角的求法,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
 (2013•汕尾二模)如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
(2013•汕尾二模)如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.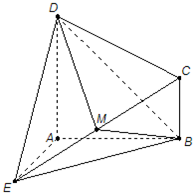 (2008•深圳一模)如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥AB,M是EC的中点.
(2008•深圳一模)如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥AB,M是EC的中点. (2010•泰安二模)如图,在△ABC中,已知∠ABC=45°,O在AB上,且
(2010•泰安二模)如图,在△ABC中,已知∠ABC=45°,O在AB上,且
