题目内容
 (2013•汕尾二模)如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
(2013•汕尾二模)如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.(Ⅰ)求证:DA⊥平面PAB;
(Ⅱ) 求直线PC与平面ABCD所成角的正弦值.
分析:(1)由∠PBC=90°得BC⊥PB,又BC⊥AB,故BC⊥平面PAB,因为AD∥BC,故AD⊥平面PAB;
(2)过点P作平面ABCD的垂线,垂足为H,连接CH,可证得∠PCH为PC与底面ABCD所成的角,在直角三角形PAH,直角三角形BCH,直角三角形PCH中分别求得PH,CH,PC的长,即可求得直线PC与平面ABCD所成角的正弦值为
.
(2)过点P作平面ABCD的垂线,垂足为H,连接CH,可证得∠PCH为PC与底面ABCD所成的角,在直角三角形PAH,直角三角形BCH,直角三角形PCH中分别求得PH,CH,PC的长,即可求得直线PC与平面ABCD所成角的正弦值为
| ||
| 8 |
解答:解:(Ⅰ)平面PAD⊥平面PAB
∵∠PBC=90°∴BC⊥PB
∵四棱锥P-ABCD的底面ABCD为矩形∴BC⊥AB
∵PB?平面PAB,AB?平面PAB,且PB∩AB=B
∴BC⊥平面PAB
∵AD∥BC
∴AD⊥平面PAB
(Ⅱ)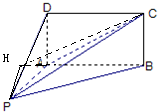 如图,过点P作BA延长线的垂线PH,垂足为H,连接CH.
如图,过点P作BA延长线的垂线PH,垂足为H,连接CH.
由(Ⅰ)可知AD⊥平面PAB
∵AD?平面ABCD
∴平面PAB⊥平面ABCD
∵PH?平面PAB,平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB
∴PH⊥平面ABCD
∴CH为PC在平面ABCD内的射影.
∴∠PCH为PC与底面ABCD所成的角.
∵∠PAB=120°
∴∠PAH=60°
∵PA=1
∴在直角三角形PAH中,PH=PA×sin60°=
,AH=PA×cos60°=
在直角三角形HBC中,BH=AH+AB=
+2=
,BC=AD=1
故CH=
=
=
在直角三角形PHC中,PC=
=
=2
∴sin∠PCH=
=
=
=
故直线PC与平面ABCD所成角的正弦值为
∵∠PBC=90°∴BC⊥PB
∵四棱锥P-ABCD的底面ABCD为矩形∴BC⊥AB
∵PB?平面PAB,AB?平面PAB,且PB∩AB=B
∴BC⊥平面PAB
∵AD∥BC
∴AD⊥平面PAB
(Ⅱ)
 如图,过点P作BA延长线的垂线PH,垂足为H,连接CH.
如图,过点P作BA延长线的垂线PH,垂足为H,连接CH.由(Ⅰ)可知AD⊥平面PAB
∵AD?平面ABCD
∴平面PAB⊥平面ABCD
∵PH?平面PAB,平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB
∴PH⊥平面ABCD
∴CH为PC在平面ABCD内的射影.
∴∠PCH为PC与底面ABCD所成的角.
∵∠PAB=120°
∴∠PAH=60°
∵PA=1
∴在直角三角形PAH中,PH=PA×sin60°=
| ||
| 2 |
| 1 |
| 2 |
在直角三角形HBC中,BH=AH+AB=
| 1 |
| 2 |
| 5 |
| 2 |
故CH=
| BH2+BC2 |
(
|
| ||
| 2 |
在直角三角形PHC中,PC=
| PH2+CH2 |
(
|
| 2 |
∴sin∠PCH=
| PH |
| PC |
| ||||
2
|
| ||
4
|
| ||
| 8 |
故直线PC与平面ABCD所成角的正弦值为
| ||
| 8 |
点评:本题主要考查了两个平面垂直的判定定理、性质定理及直线与平面所成的角概念和求法,培养了空间想象能力及问题的等价转换的能力.

练习册系列答案
相关题目

 (2013•汕尾二模)如图所示:有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.
(2013•汕尾二模)如图所示:有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上. (2013•汕尾二模)已知正方体被过一面对角线和它对面两棱中点的平面截去一个三棱台后的几何体的主(正)视图和俯视图如下,则它的左(侧)视图是( )
(2013•汕尾二模)已知正方体被过一面对角线和它对面两棱中点的平面截去一个三棱台后的几何体的主(正)视图和俯视图如下,则它的左(侧)视图是( )