题目内容

若（a-2x）5展开式中x2的系数为40，且(a-2x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5．
（1）求(a0+a2+a4)2-(a1+a3+a5)2的值；
（2）求|a0|+|a1|+|a2|+|a3|+|a4|+|a5|的值；
（3）求a1+2a2+3a3+4a4+5a5的值．
由题知
C25
a3（-2x）2=40a3x2，
∴40a3=40，∴a=1，
即（a-2x）5=（1-2x）5，
设f（x）=（1-2x）5，
（1）(a0+a2+a4)2-(a1+a3+a5)2=（a0+a1+…+a5）（a0-a1+…-a5）=f（1）f（-1）=-35=-243．
（2）令g（x）=（1+2x）5，
则|a0|+|a1|+…+|a5|=g（1）=35=243；
（3）由于f（x）=（1-2x）5=a0+a1x+a2x2+…+a5x5，
∴f′（x）=-10（1-2x）4=a1+2a2x+3a3x2+4a4x3+5a5x4，
∴f′（1）=-10（1-2）4=a1+2a2+3a3+4a4+5a5=-10．
练习册系列答案
相关题目
已知在(
3x
-
1
2
3x
)n的展开式中，第5项为常数项．
（1）求n；
（2）求展开式中含x2的项．
在二项式（x-
1
x2
）6的展开式中，常数项是（　　）
A．-10B．-15C．10D．15
已知（
x
+
1
2•
4x
）n的展开式前三项中的x的系数成等差数列．
（1）展开式中所有的x的有理项为第几项？
（2）求展开式中系数最大的项．
二项式（1+sinx）n的展开式中，末尾两项的系数之和为7，且二项式系数最大的一项的值为
5
2
，则x在（0，2π）内的值为______．
已知（
x
-
1
2x
）n的展开式中，前三项系数的绝对值依次成等差数列，
（1）求n
（2）设（2x-1）n=a0+a1x+a2x2+…+anxn，求：①a1+a2+a3+…+an ②a1+2a2+3a3+…+nan．
在（x+y）n的展开式中，若第九项系数最大，则n的值可能等于（　　）
A．14，15B．15，16C．16，17D．14，15，16
某电视台的一个智力游戏节目中，有一道将中国四大名著《三国演义》、《水浒传》、《西游记》、《红楼梦》与它们的作者连线的题目，每本名著只能与一名作者连线，每名作者也只能与一本名著连线，每连对一个得2分，连错得－1分，某观众只知道《三国演义》的作者是罗贯中，其他不知道随意连线，将他的得分记作ξ.
(1)求该观众得分ξ为负数的概率；
(2)求ξ的分布列．
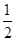某学生参加某高校的自主招生考试，须依次参加A，B，C，D，E五项考试，如果前四项中有两项不合格或第五项不合格，则该考生就被淘汰，考试即结束；考生未被淘汰时，一定继续参加后面的考试．已知每一项测试都是相互独立的，该生参加A，B，C，D四项考试不合格的概率均为，参加第五项不合格的概率为.
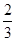(1)求该生被录取的概率；
(2)记该生参加考试的项数为X，求X的分布列和期望．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网