题目内容

2．已知正方体ABCD-A1B1C1D1，过A1点可作    条直线与直线AC和BC1都成60°角（　　）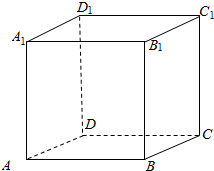
A．1B．2C．3D．4

分析 因为AD1∥BC1，过A1在空间作直线l，使l与直线AC和BC1所成的角都等于 600，可转化为过点A在空间作直线l，使l与直线AC和AD1所成的角都等于 600．可分在平面ACD1内和在平面ACD1外两种情况寻找．因为要与直线AC和AD1所成的角都相等，故在平面ACD1内可考虑角平分线；在平面AC11外可将角平分线绕点A旋转考虑．

解答 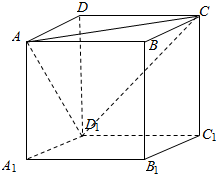解：因为AD1∥BC1，所以过A1在空间作直线l，使l与直线AC和BC1所
成的角都等于 60°，即过点A在空间作直线l，使l与直线AC和AD1所
成的角都等于 60°．
因为∠CAD1=60°，∠CAD1的外角平分线与AC和AD1所成的角相等，
均为60°，所以在平面ACD1内有一条满足要求．
因为∠CAD1的角平分线与AC和AD1所成的角相等，均为30°，
将角平分线绕点A向上转动到与面ACD1垂直的过程中，
存在两条直线与直线AC和AD1所成的角都等于 60°；
故符合条件的直线有3条．
故选：C．

点评 本题考查异面直线所成角的问题，考查空间想象能力和转化能力．在解决本题的过程中，转化思想很重要，属于中档题．

练习册系列答案
相关题目
12．在复平面内，复数$\frac{-2-3i}{i}$对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
13．若cosα＞0，则（　　）
A．tanαsinα≥0B．sin2α≤0C．sinα≤0D．cos2α＜0
10．已知函数 f（x）的定义域为 A，若当f（x1）=f（x2）（x1，x2∈A）时，总有x1=x2，则称 f（x）为单值函数．例如，函数f（x）=2x+1（x∈R）是单值函数．给出下列命题：
①函数f（x）=x2（x∈R）是单值函数；
②函数f（x）=2x（x∈R）是单值函数；③若f（x）为单值函数，x1，x2∈A，且x1≠x2，则f（x1）≠f（x2）；
④函数f（x）=$\left\{\begin{array}{l}{\sqrt{x}，x≥0}\\{（\frac{1}{2}）^{x}-1，x＜0}\end{array}\right.$是单值函数．
其中的真命题是②③．（写出所有真命题的编号）
17．下列说法中正确的个数有（　　）
①两平面平行，夹在两平面间的平行线段相等；
②两平面平行，夹在两平面间的相等的线段平行；
③两条直线被三个平行平面所截，截得的线段对应成比例；
④如果夹在两平面间的三条平行线段相等，那么这两个平面平行．
A．1个B．2个C．3个D．4个
7．各项为正数的数列{an} 的前n项和为Sn，且满足：Sn=$\frac{1}{4}$an2+$\frac{1}{2}$an+$\frac{1}{4}$（n∈N+）．
（Ⅰ）求an；
（Ⅱ）设函数f（n）=$\left\{\begin{array}{l}{{a}_{n}，n为奇数}\\{f（\frac{n}{2}），n为偶数}\end{array}\right.$，Cn=f（2n+4）（n∈N+），求数列{Cn}的前n项和Tn．．
14．函数f（x）=loga（4x-x2-3）（0＜a＜1）的单调增区间是（2，3）．
11．若函数f（x+1）的定义域是[-2，4]，则函数f（2x-1）的定义域是[0，3]．
12．函数f（x）=ln（2x+$\sqrt{4{x}^{2}+1}$）的奇偶性是（　　）
A．奇函数B．偶函数
C．既不是奇函数也不是偶函数D．既是奇函数也是偶函数

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网