题目内容
16.不等式组$\left\{\begin{array}{l}{x+3(5-x)>2}\\{x-3>\frac{x}{2}-\frac{1}{4}}\end{array}\right.$的解集是{x|$\frac{11}{2}$<x<$\frac{13}{2}$}.分析 分别求出每个不等式的解集,然后求其交集即可.
解答 解:由x+3(5-x)>2,解得x<$\frac{13}{2}$,
由x-3>$\frac{x}{2}$-$\frac{1}{4}$,解得x>$\frac{11}{2}$,
∴不等式组的解为$\frac{11}{2}$<x<$\frac{13}{2}$,
∴不等式组的解集为{x|$\frac{11}{2}$<x<$\frac{13}{2}$}.
故答案为:{x|$\frac{11}{2}$<x<$\frac{13}{2}$}.
点评 本题考查了不等式组的解集的求法,属于基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
7.设P是不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+3y≤1}\end{array}\right.$表示的平面区域内的任意一点,向量$\overrightarrow{m}$=(-1,1),$\overrightarrow{n}$=(2,-1),若$\overrightarrow{OP}=λ\overrightarrow m+μ\overrightarrow n$,则$\frac{μ}{λ+1}$的取值范围( )
| A. | [-$\frac{1}{2}$,2] | B. | [0,1] | C. | [$\frac{1}{2}$,1] | D. | [0,$\frac{1}{2}$] |
1.设a>-b,则下列不等式中,成立的是( )
| A. | a(a+b)2<-b(a+b)2 | B. | a(a+b)2>-b(a+b)2 | C. | a(a+b)2≤-b(a+b)2 | D. | a(a+b)2≥-b(a+b)2 |
1.定义移动运算“⊕”,对于任意正整数n满足以下运算:(1)1⊕1=1;(2)(n+1)⊕1=2+n⊕1,则n⊕1用含n的代数式可表示为( )
| A. | 2n-1 | B. | n | C. | 2n-1 | D. | 2n-1 |
19.已知双曲线$\frac{x^2}{4}-{y^2}=1$,过点O(0,0)作直线l与双曲线仅有一个公共点,这样的直线l共有( )
| A. | 0条 | B. | 2条 | C. | 4条 | D. | 无数条 |
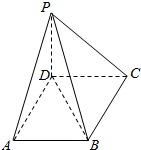 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PD⊥底面ABCD,AB=2AD,∠ADB=90°,
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PD⊥底面ABCD,AB=2AD,∠ADB=90°,