题目内容
已知：M={a|函数
在[
]上是增函数}，N={b|方程
有实数解}，设D=
，且定义在R上的奇函数
在D内没有最小值，则m的取值范围是 ．
【答案】
m>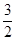
【解析】
试题分析：先确定出集合MN的范围，求出集合D的范围．再根据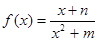
在D内没有最小值，对函数的最小值进行研究，可先求其导数，利用导数研究出函数的单调性，确定出函数的最小值在区间D的左端点取到即可，由于直接研究有一定困难，可将函数变为
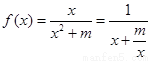，构造新函数h（x）=
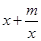，将研究原来函数没有最小值的问题转化为新函数没有最大值的问题，利用导数工具易确定出新函数的最值，从而解出参数m的取值范围m>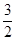,若m≤0，可得函数f（x）在D上是减函数，函数在右端点
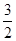处取到最小值，不合题意；若m＞0，令h（x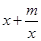）=，则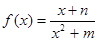在D内没有最小值可转化为h（x）在D内没有最大值，下对h（x）在D内的最大值进行研究，可知答案为m>。
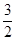考点：函数的单调性与其导函数的正负
点评：本题主要考查函数的单调性与其导函数的正负情况之间的关系，三角函数的周期求法及对三角函数图象特征的理解，指数函数的值域及集合的运算．考查了转化的思想及分类讨论的思想，计算的能力，本题综合性强涉及到的知识点较多，属于综合题中的难题
练习册系列答案
阶梯计算系列答案
相关题目
]上是增函数}，N={b|方程3-|x-1|-b+1=0有实数解}，设D=M∩N，且定义在R上的奇函数
在D内没有最小值，则m的取值范围是 ．
]上是增函数}，N={b|方程3-|x-1|-b+1=0有实数解}，设D=M∩N，且定义在R上的奇函数
在D内没有最小值，则m的取值范围是 ．