题目内容
已知：集合A={x|y=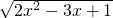
}，B={y|y=x2-2x-3，x∈R}，则CR（A∩B ）=________．
（-∞，-4）∪（
，1）
分析：由函数的定义域解出集合A，再由二次函数的值域解出集合B；由交集的定义求A∩B，再由补集的含义求CR（A∩B），求解即得．
解答：A={x|y=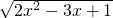}={x|2x2-3x+1≥0}={x|x≤或x≥1}，
B={y|y=x2-2x-3，x∈R}={y|y≥-4，x∈R}=[-4，+∞）．
∴A∩B={x|-4≤x
或x≥1}，
所以CR（A∩B）=（-∞，-4）∪（，1）
故答案为：（-∞，-4）∪（，1）．
点评：本题考查函数的定义域、值域、二次不等式的求解、集合的运算等知识，属基本题型、基本运算的考查．
，1）分析：由函数的定义域解出集合A，再由二次函数的值域解出集合B；由交集的定义求A∩B，再由补集的含义求CR（A∩B），求解即得．
解答：A={x|y=
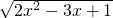}={x|2x2-3x+1≥0}={x|x≤或x≥1}，B={y|y=x2-2x-3，x∈R}={y|y≥-4，x∈R}=[-4，+∞）．
∴A∩B={x|-4≤x
或x≥1}，所以CR（A∩B）=（-∞，-4）∪（
，1）故答案为：（-∞，-4）∪（
，1）．点评：本题考查函数的定义域、值域、二次不等式的求解、集合的运算等知识，属基本题型、基本运算的考查．
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目