Question

方程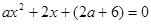至少有一个负实数根的充要条件是a _______

 

Answer 1

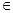【答案】

(-3,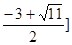

【解析】

试题分析：根据所给的方程的特征项的系数是一个字母，需要先对二次项系数分为0和不为0两种情况讨论，在二次项系数不为0时又分两根一正一负和两根均为负值两种情况，综合在一起找到a所满足的条件。

当a=0得到x=-3符合题意．

当a≠0时，显然方程没有等于零的根．

若方程有两异号实根，根据根与系数之间的关系得到a＜0；

若方程有两个负的实根，由根与系数之间的关系得到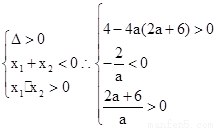，可知参数a的范围是(-3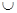, 0)（0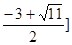，，综上可知为(-3,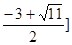

考点：本题主要考查了一元二次方程实根分布问题即充要条件问题。

点评：本题解题的关键是对于特征项的系数等于0的情况不要忽略，要熟练应用根与系数的关系，本题是一个易错题．