Question

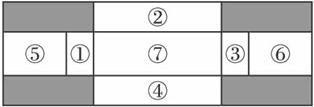
将一张2×6米的硬钢板按图纸的要求进行操作：沿线裁去阴影部分，把剩余部分按要求焊接成一个有盖的长方体水箱（⑦为底，①②③④为侧面，⑤+⑥为水箱盖.其中①与③、②与④分别是全等的矩形，且⑤+⑥=⑦），设水箱的高为x米，容积为y立方米.

（1）写出y关于x的函数关系式；

（2）如何设计x的大小，使得水箱的容积最大？

Answer 1

解：（1）依题意,水箱底的宽为(2-2x)米，长为=(3-x)米,

则水箱的容积y=(2-2x)(3-x)·x(0＜x＜1),即为y关于x的函数关系式.

（2）y=(2-2x)(3-x)·x=2x³-8x²+6x(0＜x＜1),

∴y′=6x²-16x+6.令y′=6x²-16x+6=0得x=,

当0＜x＜时y′＞0，函数单调递增;

当＜x＜1时y′＜0,函数单调递减,

∴当x=时函数y=(2-2x)(3-x)·x(0＜?x＜?1)取得最大值.

∴设计x=，水箱的容积最大.