题目内容
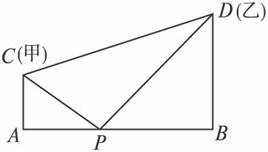
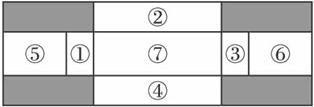
 将一张2×6米的硬钢板按图纸的要求进行操作,沿线裁去阴影部分,把剩余部分按要求焊接成一个有盖的长方体水箱(其中①与③、②与④分别是全等的矩形,且⑤+⑥=⑦),设水箱的高为x米,容积为y立方米.
将一张2×6米的硬钢板按图纸的要求进行操作,沿线裁去阴影部分,把剩余部分按要求焊接成一个有盖的长方体水箱(其中①与③、②与④分别是全等的矩形,且⑤+⑥=⑦),设水箱的高为x米,容积为y立方米.(1)求y关于x的函数关系式;
(2)如何设计x的大小,使得水箱装的水最多?
分析:(1)根据①与③、②与④分别是全等的矩形,且⑤+⑥=⑦),可得水箱底面长宽,从而可表示水箱的容积,即y关于x的函数关系式;
(2)利用导数求最值,由于函数的单峰函数,故在导数为0处取极值,且为最值.
(2)利用导数求最值,由于函数的单峰函数,故在导数为0处取极值,且为最值.
解答:解:(1)设水箱的高为x(米),则水箱底面长宽分别为
=3-x(米),2-2x(米)
故水箱的容积为y=2x(3-x)(1-x)=2x3-8x2+6x(0<x<1)
(2)由y'=6x2-16x+6=0,得:x=
所以:y=2x3-8x2+6x(0<x<1)在(0,
)上单调递增,在(
,1)上单调递减
所以x=
时水箱的容积最大.
| 6-2x |
| 2 |
故水箱的容积为y=2x(3-x)(1-x)=2x3-8x2+6x(0<x<1)
(2)由y'=6x2-16x+6=0,得:x=
4±
| ||
| 3 |
所以:y=2x3-8x2+6x(0<x<1)在(0,
4-
| ||
| 3 |
4-
| ||
| 3 |
所以x=
4-
| ||
| 3 |
点评:本题以实际问题为载体,考查函数模型的构建,考查导数法求函数的最值,有一定的综合性.

练习册系列答案
相关题目