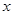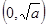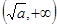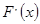题目内容
已知函数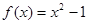 与函数
与函数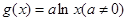 .
.
(I)若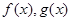 的图象在点
的图象在点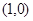 处有公共的切线,求实数
处有公共的切线,求实数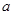 的值;
的值;
(II)设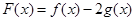 ,求函数
,求函数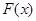 的极值.
的极值.
【答案】
⑴a=2;
⑵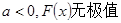
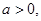
|
|
|
|
|
|
|
- |
0 |
+ |
|
|
|
极小值 |
|
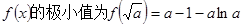 .
.
【解析】本试题主要是考查了导数的几何意义的运用,以及运用导数的思想来判定一函数极值的综合运用。
(1)因为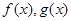 的图象在点
的图象在点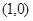 处有公共的切线,,因此则在该点处的导数值相等,得到参数a的值。
处有公共的切线,,因此则在该点处的导数值相等,得到参数a的值。
(2)因为)设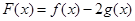 ,分别对参数a进行分类讨论,得到函数
,分别对参数a进行分类讨论,得到函数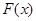 的极值.
的极值.
⑴a=2 -------4分
⑵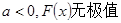 -------6分
-------6分
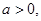
|
|
|
|
|
|
|
- |
0 |
+ |
|
|
|
极小值 |
|
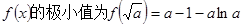 -------12分
-------12分

练习册系列答案
相关题目