题目内容
计算题(1)(0.25)
| 1 |
| 2 |
| 3 |
| 7 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
(2)(lg5)2+lg2×lg50.
分析:(1)将小数化为分数,利用分数指数幂的运算法则化简式子,即可求出所求;
(2)由式子的特点把50拆成5与10的乘积,则lg50=lg10+lg5,再利用lg5+lg2=1进行化简求值.
(2)由式子的特点把50拆成5与10的乘积,则lg50=lg10+lg5,再利用lg5+lg2=1进行化简求值.
解答:解:(1)(0.25)
-[-2×(
)0]2×[(-2)3]
+(
-1)-1-2
=
-4×16+
+1-
=-
(6分)
(2)(lg5)2+lg2×lg50
=(lg5)2+lg2×(lg10+lg5)
=(lg5)2+lg2+(lg5)(lg2)
=lg5(lg5+lg2)+lg2=1(6分)
| 1 |
| 2 |
| 3 |
| 7 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 2 |
| 2 |
| 125 |
| 2 |
(2)(lg5)2+lg2×lg50
=(lg5)2+lg2×(lg10+lg5)
=(lg5)2+lg2+(lg5)(lg2)
=lg5(lg5+lg2)+lg2=1(6分)
点评:本题考查了根式与分数指数幂的互化及其化简运算、以及对数的运算性质的应用,一般是把真数拆成两数积或商的形式,或是把多个对数合成一个对数;以及等式“lg2+lg5=1”的利用.

练习册系列答案
相关题目
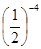 -4÷
-4÷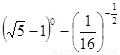 ;
;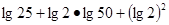 .
.