题目内容
各项均为正数的等比数列{an}中,已知a2="8," a4="128," bn=log2an .
(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Sn
(3)求满足不等式 的正整数n的最大值
的正整数n的最大值
【答案】
(1)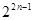 (2)2013
(2)2013
【解析】
试题分析:解:(1)∵ 等比数列{an}的各项为正,a2="8," a4="128"
设公比为q
∴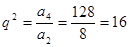 q="4" a1="2" ∴an=a1qn-1=2×
q="4" a1="2" ∴an=a1qn-1=2×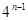 =
=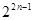 (4分)
(4分)
(2)∵
∴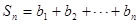 =
=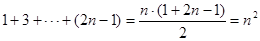 (8分)
(8分)
(3) ∵(1-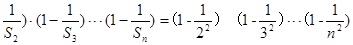
=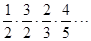
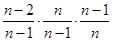 =
=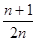
∴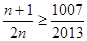 ∴n≤2013 ∴n的最大值为2013 (12分)
∴n≤2013 ∴n的最大值为2013 (12分)
考点:等比数列
点评:主要是考查了等比数列的通项公式法运用,以及数列的求解积的运算,属于基础题。

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目