题目内容
设函数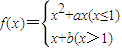
，若该函数在实数集R上可导，求实数a、b的值和该函数的最小值．
【答案】分析：由题意函数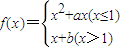
，对其进行分段求导，求出a，b的值，然后根据二次函数的性质求出最小值．
解答：解：依题意f'（1）=2+a=1，且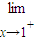
f（x）=f（1）=1+a，
∴a=b=-1，
∴f（x）=
，
当x＞1时，f（x）＞0，
当x≤1时，f（x）=x2-x=（x-
）2-
≥-
，
∴可得函数的最小值是f（
）=-
．
点评：此题主要考查导数的概念及函数最值的求法，还有分段函数的应用，是一道比较基础的题．
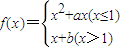，对其进行分段求导，求出a，b的值，然后根据二次函数的性质求出最小值．解答：解：依题意f'（1）=2+a=1，且
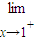f（x）=f（1）=1+a，∴a=b=-1，
∴f（x）=
，当x＞1时，f（x）＞0，
当x≤1时，f（x）=x2-x=（x-
）2-≥-，∴可得函数的最小值是f（
）=-．点评：此题主要考查导数的概念及函数最值的求法，还有分段函数的应用，是一道比较基础的题．
练习册系列答案
相关题目