题目内容
已知函数
(I)当a=1时,求函数f(x)的最小值;
(II)当a≤0时,讨论函数f(x)的单调性;
(III)是否存在实数a,对任意的x1,x2 (0,+∞),且x1≠x2,都有
(0,+∞),且x1≠x2,都有 恒成立.若存在,求出a的取值范围;若不存在,说明理由.
恒成立.若存在,求出a的取值范围;若不存在,说明理由.
【答案】
(I)-2ln2
(II)当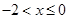 时,
时,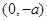 和
和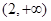 为单调增区间,
为单调增区间,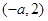 为单调减区间;当a=-2时,
为单调减区间;当a=-2时,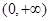 为单调增区间;当a<-2时,
为单调增区间;当a<-2时,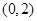 和
和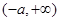 为单调增区间,
为单调增区间,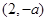 为单调减区间.
为单调减区间.
(III)存在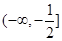 .
.
【解析】
试题分析:(I)
首先确定函数的定义域,然后求导,根据函数导函数的性质,确定函数的单调区间,判断极小值就是最小值,求出即可. (II) 求导、同分整理得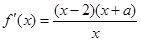 .再分当
.再分当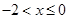 或当a=-2或a<-2时,判断
或当a=-2或a<-2时,判断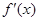 的符号,确定函数单调区间即可. (III) 假设存在实数a使得对任意的
的符号,确定函数单调区间即可. (III) 假设存在实数a使得对任意的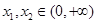 ,且
,且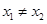 ,都有
,都有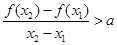 恒成立. 不妨设
恒成立. 不妨设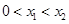 ,使得
,使得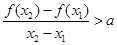 ,即
,即 ,构造函数令
,构造函数令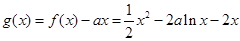 ,利用导函数求出满足函数g(x)在
,利用导函数求出满足函数g(x)在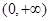 为增函数的a取值范围即可.
为增函数的a取值范围即可.
试题解析:解:(I)定义域为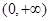 ,当a=1时,
,当a=1时,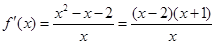 ,所以当
,所以当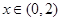 时,
时,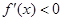 ,
,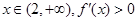 ,所以f(x)在x=2时取得最小值,其最小值为
,所以f(x)在x=2时取得最小值,其最小值为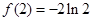 .
.
(II) 因为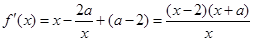 ,所以
,所以
(1)当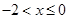 时,若
时,若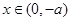 ,
,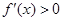 ,f(x)为增函数;
,f(x)为增函数;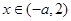 时,
时,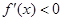 ,f(x)为减函数;
,f(x)为减函数;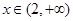 时,
时,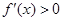 ,f(x)为增函数;
,f(x)为增函数;
(2)当a=-2时,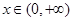 ,f(x)为增函数;
,f(x)为增函数;
(3)当a<-2时,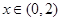 时,
时,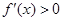 ,f(x)为增函数;
,f(x)为增函数;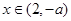 时,
时,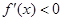 ,f(x)为减函数;
,f(x)为减函数;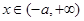 ,
,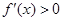 ,f(x)为增函数;
,f(x)为增函数;
(III)假设存在实数a使得对任意的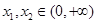 ,且
,且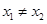 ,都有
,都有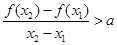 恒成立,不妨设
恒成立,不妨设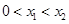 ,使得
,使得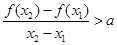 ,即
,即 ,
,
令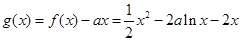 ,只要g(x)在
,只要g(x)在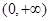 为增函数,考察函数
为增函数,考察函数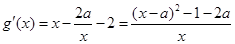 ,要使
,要使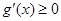 在
在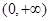 恒成立.只需
恒成立.只需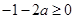 ,即
,即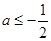 ,故存在实数
,故存在实数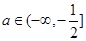 符合题意.
符合题意.
考点:1.导数法;2.函数的单调性;3、不等式恒成立.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
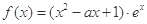 .
.