题目内容
若α、β终边关于y轴对称，则下列等式成立的是（ ）A．sinα=sinβ
B．cosα=cosβ
C．tanα=tanβ
D．sinα=-sinβ
【答案】分析：在角α终边上任取一点P（x，y），点P关于y轴对称的点为P′（-x，y）在β的终边上，依据三角函数的定义求sinα和sinβ．
解答：解：∵α、β终边关于y轴对称，设角α终边上一点P（x，y），
则点P关于y轴对称的点为P′（-x，y），
且点P与点P′到原点的距离相等，
设为r，则 P′（-x，y）在β的终边上，
由三角函数的定义得 sinα=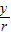
，s inβ=
，
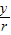∴sinα=sinβ，
故选A．
点评：本题考查任意角的三角函数的定义以及直线关于直线的对称直线，点关于直线的对称点问题．
解答：解：∵α、β终边关于y轴对称，设角α终边上一点P（x，y），
则点P关于y轴对称的点为P′（-x，y），
且点P与点P′到原点的距离相等，
设为r，则 P′（-x，y）在β的终边上，
由三角函数的定义得 sinα=
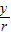，s inβ=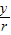，∴sinα=sinβ，
故选A．
点评：本题考查任意角的三角函数的定义以及直线关于直线的对称直线，点关于直线的对称点问题．
练习册系列答案
相关题目
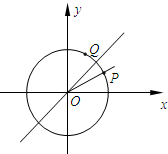如图，已知单位圆上两点P，Q关于直线y=x对称，且以射线OP为终边的角的大小为x．
