题目内容
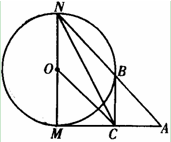
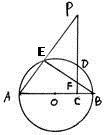
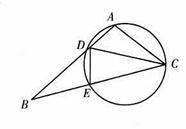
如图△ 为直角三角形,
为直角三角形,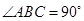 ,以
,以 为直径的圆交
为直径的圆交 于点
于点 ,点
,点 是
是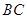 边的中点,连
边的中点,连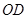 交圆
交圆 于点
于点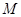 .
.
(Ⅰ)求证: 、
、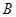 、
、 、
、 四点共圆;
四点共圆;
(Ⅱ)设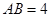 ,
,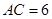 ,求
,求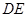 的长.
的长.
(1)(1)做出辅助线,首先证明两个三角形全等,根据三角形三边对应相等,得到两个三角形全等,得到对应角相等,从而得到四边形一对对角互补,即四点共圆.
(2)5
解析试题分析:(1)证明:连结OE,BE
∵AB为圆O直径 ∴BE⊥AE
OB=OE ∴∠BEO=∠OBE
Rt△BEC中 D为BC中点 ∴BD=DE ∠BED=∠DBE
∠OED=∠BEO+∠BED=∠OBE+∠DBE=∠OBD=∠ABD=90°
∠OED+∠OBD=180°
∴O、B、D、E四点共圆 5分
(II)解:延长DO交圆于H, O、D分别为AB、AC中点
OD=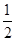 AC=3 MH=AB=4 DM=1
AC=3 MH=AB=4 DM=1
由(I)OE⊥DE E为圆上 ∴DE为圆O切线
DE2=DM·DH=1·(4+1)=5 10分
考点:三角形全等,四点共圆
点评:本题考查三角形全等,考查四点共圆,考查圆的切割线定理,是一个平面几何的综合题目,解题时注意分析要证明的结论与条件之间的关系

练习册系列答案
相关题目
 的外接圆为⊙
的外接圆为⊙ ,
,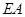 是⊙
是⊙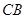 的延长线与
的延长线与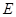 ,
,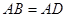 .
.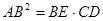 .
.
 与圆
与圆 内切于点
内切于点 ,其半径分别为
,其半径分别为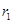 与
与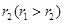 ,圆
,圆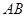 交圆
交圆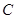 (
( 为定值。
为定值。
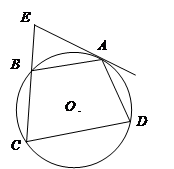
 是圆内接四边形,延长
是圆内接四边形,延长 与的延长线
与的延长线 交于点
交于点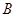 ,且
,且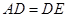 ,
, 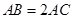 .
.
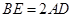 ;
;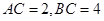 时,求
时,求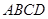 是☉
是☉ 的内接四边形,
的内接四边形, 不经过点
不经过点 平分
平分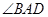 ,经过点
,经过点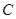 的直线分别交
的直线分别交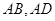 的延长线于点
的延长线于点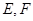 ,且
,且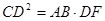 ,证明:
,证明: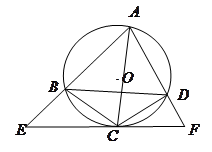
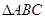 ∽
∽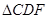 ;
; 是☉
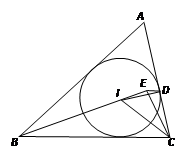
是☉ 为锐角△
为锐角△ 的内心,且
的内心,且 ,点
,点 为内切圆
为内切圆 的切点,过点
的切点,过点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 .
.
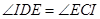 ;
;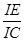 的值.
的值. 经过
经过 ⊙O上一点
⊙O上一点 ,且
,且 ,
,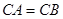 ,⊙O交直线
,⊙O交直线 于
于 .
.
 ⊙O的半径为3,求
⊙O的半径为3,求 的长.
的长.