题目内容
消去未知数“y”,化
(k为已知常数)为只有“x”的一元二次方程为
|
(1+4k2)x2-8
k2x+12k2-4=0
| 3 |
(1+4k2)x2-8
k2x+12k2-4=0
.| 3 |
分析:为了得到只有“x”的一元二次方程,只须将y=k(x-
)代入x2+4y2-4=0中,消去y后得x2+4[k(x-
)]2-4=0,再利用平方和公式化简即可.
| 3 |
| 3 |
解答:解:将y=k(x-
)代入x2+4y2-4=0中,得
x2+4[k(x-
)]2-4=0,
利用平方和公式化简,得(1+4k2)x2-8
k2x+12k2-4=0.
故答案为:(1+4k2)x2-8
k2x+12k2-4=0.
| 3 |
x2+4[k(x-
| 3 |
利用平方和公式化简,得(1+4k2)x2-8
| 3 |
故答案为:(1+4k2)x2-8
| 3 |
点评:本小题主要考查消元法等基础知识,考查运算求解能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
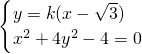 (k为已知常数)为只有“x”的一元二次方程为________.
(k为已知常数)为只有“x”的一元二次方程为________. (k为已知常数)为只有“x”的一元二次方程为 .
(k为已知常数)为只有“x”的一元二次方程为 .