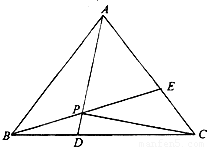
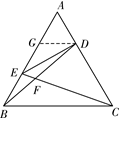
题目内容
如图,在正△ABC中,点D,E分别在边AC, AB上,且AD= AC, AE=
AC, AE=  AB,BD,CE相交于点F。
AB,BD,CE相交于点F。
(I)求证:A,E,F,D四点共圆;
(Ⅱ)若正△ABC的边长为2,求,A,E,F,D所在圆的半径.
(Ⅰ)证明:见解析;(Ⅱ)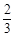 。
。
解析试题分析:(Ⅰ)证明: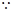
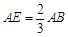 ,
,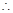
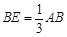 .
. 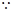 在正△
在正△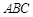 中,
中, ,
,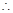
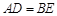 ,
,
又 ,
,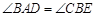 ,
, 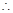 △BAD≌△CBE,
△BAD≌△CBE,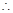
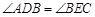 ,
,
即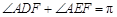 ,所以
,所以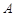 ,
,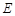 ,
,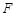 ,
,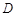 四点共圆.
四点共圆.
(Ⅱ)解:如图,取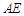 的中点
的中点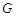 ,连结
,连结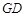 ,则
,则 .
.
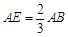 ,
,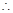
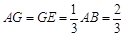 ,
,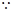
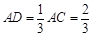 ,
,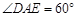 ,
,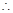 △AGD为正三角形,
△AGD为正三角形,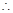
 ,即
,即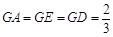 ,
,
所以点 是△AED外接圆的圆心,且圆
是△AED外接圆的圆心,且圆 的半径为
的半径为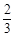 .
.
由于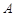 ,
,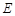 ,
,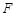 ,
,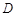 四点共圆,即
四点共圆,即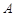 ,
,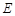 ,
,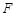 ,
,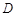 四点共圆
四点共圆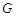 ,其半径为
,其半径为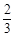 。
。
考点:本题主要考查平面几何选讲,三角形及圆的问题。
点评:本题通过考查四点共圆、三角形全等,全面考查了平面几何选讲问题,中档题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 如图,在正△ABC中,点D,E分别在边AC,AB上,且AD=
如图,在正△ABC中,点D,E分别在边AC,AB上,且AD= 选修4-1:几何证明选讲如图,在正△ABC中,点D,E分别在边t上,且
选修4-1:几何证明选讲如图,在正△ABC中,点D,E分别在边t上,且 AC, AE=
AC, AE=  AB,BD,CE相交于点F。
AB,BD,CE相交于点F。
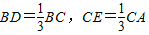 ,AD,BE相交于点P,
,AD,BE相交于点P,