题目内容
已知集合S={x|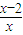 <0},T={x|x2-(2a+1)x+a2+a≥0} (a∈R),若S∪T=R,则实数a的取值范围是( )
<0},T={x|x2-(2a+1)x+a2+a≥0} (a∈R),若S∪T=R,则实数a的取值范围是( )A.-1≤a≤1
B.-1<a≤1
C.0≤a≤1
D.0<a≤1
【答案】分析:由已知中集合S={x|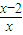 <0},T={x|x2-(2a+1)x+a2+a≥0} (a∈R),我们易求出集合,再由S∪T=R,我们易构造出一个关于a的不等式组,解不等式组,即可得到实数a的取值范围.
<0},T={x|x2-(2a+1)x+a2+a≥0} (a∈R),我们易求出集合,再由S∪T=R,我们易构造出一个关于a的不等式组,解不等式组,即可得到实数a的取值范围.
解答:解:∵集合S={x|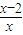 <0}={x|0<x<2}
<0}={x|0<x<2}
T={x|x2-(2a+1)x+a2+a≥0}={x|x≥a+1或x≤a}
又∵S∪T=R,
∴a+1≤2,a≥0,
∴0≤a≤1
故选C.
点评:本题考查的知识点是集合关系中的参数取值问题,其中根据已知条件,构造出关于a的不等式组,是解答本题的关键.
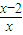 <0},T={x|x2-(2a+1)x+a2+a≥0} (a∈R),我们易求出集合,再由S∪T=R,我们易构造出一个关于a的不等式组,解不等式组,即可得到实数a的取值范围.
<0},T={x|x2-(2a+1)x+a2+a≥0} (a∈R),我们易求出集合,再由S∪T=R,我们易构造出一个关于a的不等式组,解不等式组,即可得到实数a的取值范围.解答:解:∵集合S={x|
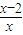 <0}={x|0<x<2}
<0}={x|0<x<2}T={x|x2-(2a+1)x+a2+a≥0}={x|x≥a+1或x≤a}
又∵S∪T=R,
∴a+1≤2,a≥0,
∴0≤a≤1
故选C.
点评:本题考查的知识点是集合关系中的参数取值问题,其中根据已知条件,构造出关于a的不等式组,是解答本题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
已知集合S={x||2x-1|<1},则使S∩T=S∪T的集合T=( )
| A、{x|0<x<1} | ||
B、{x|0<x<
| ||
C、{x|x<
| ||
D、{x|
|