题目内容
对于任意两个复数z1=x1+y1i,z2=x2+y2i(x1、y1、x2、y2为实数),定义运算⊙为:z1⊙z2=x1x2+y1y2.设非零复数w1、w2在复平面内对应的点分别为P1、P2,点为O为坐标原点.如果w1⊙w2=0,那么在△P1OP2中,∠P1OP2的大小为 .
【答案】分析:根据题意得,z1⊙z2=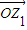 •
•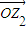 ,故有 z1⊙z2 =0 时,
,故有 z1⊙z2 =0 时,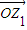 •
•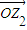 =0,OZ1⊥OZ2.所以,w1⊙w2=0时,∠P1OP2的大小为
=0,OZ1⊥OZ2.所以,w1⊙w2=0时,∠P1OP2的大小为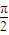 .
.
解答:解:∵z1⊙z2=x1x2+y1y2 表示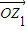 •
•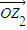 坐标运算结果,
坐标运算结果,
∴当 z1⊙z2=x1x2+y1y2=0 时,
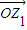 •
•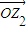 =0,即∠z1 Oz2=
=0,即∠z1 Oz2=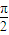 ,OZ1⊥OZ2.
,OZ1⊥OZ2.
如果w1⊙w2=0,那么在△P1OP2中,∠P1OP2的大小为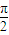 ,
,
故答案为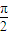 .
.
点评:本题考查新定义的意义,复数的代数表示法及其几何意义,两个向量坐标形式的数量积运算法则.
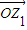 •
•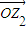 ,故有 z1⊙z2 =0 时,
,故有 z1⊙z2 =0 时,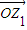 •
•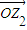 =0,OZ1⊥OZ2.所以,w1⊙w2=0时,∠P1OP2的大小为
=0,OZ1⊥OZ2.所以,w1⊙w2=0时,∠P1OP2的大小为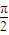 .
.解答:解:∵z1⊙z2=x1x2+y1y2 表示
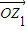 •
•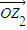 坐标运算结果,
坐标运算结果,∴当 z1⊙z2=x1x2+y1y2=0 时,
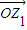 •
•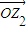 =0,即∠z1 Oz2=
=0,即∠z1 Oz2=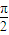 ,OZ1⊥OZ2.
,OZ1⊥OZ2.如果w1⊙w2=0,那么在△P1OP2中,∠P1OP2的大小为
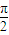 ,
,故答案为
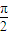 .
.点评:本题考查新定义的意义,复数的代数表示法及其几何意义,两个向量坐标形式的数量积运算法则.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目