题目内容
以下有关平面向量的结论:
①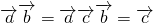 ;②
;② ;③
;③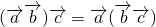 ;④
;④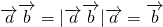 ,
,
其中正确的结论有
- A.1个
- B.2个
- C.3个
- D.4个
A
分析:根据平面向量的数量积运算、模的运算性质和平面向量基本定理,对各个选项逐个加以判断,并且结合举反例和直接证明的方法,可得只有选项②是正确的,由此可得本题的答案.
解答:因为当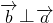 且
且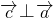 时,有
时,有 =0,但不能得出
=0,但不能得出 的结论,故①不正确;
的结论,故①不正确;
由 ,可得
,可得 -
- =0,即
=0,即 =
= ,所以
,所以 成立,故②正确;
成立,故②正确;
因为 =λ
=λ ,是一个与
,是一个与 共线的向量,而
共线的向量,而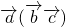 =μ
=μ ,是一个与
,是一个与 共线的向量.
共线的向量.
所以等式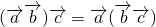 不一定成立,故③不正确;
不一定成立,故③不正确;
∵ ,θ是两向量的夹角
,θ是两向量的夹角
∴由 可得cosθ=1,可得θ=0.说明向量
可得cosθ=1,可得θ=0.说明向量 、
、 共线且同向,不一定相等,故④不正确.
共线且同向,不一定相等,故④不正确.
故正确的选项只有②,1个
故答案为:A
点评:本题以命题的真假判断为载体,着重考查了平面向量的数量积运算、模的运算性质和平面向量基本定理等知识,属于基础题.
分析:根据平面向量的数量积运算、模的运算性质和平面向量基本定理,对各个选项逐个加以判断,并且结合举反例和直接证明的方法,可得只有选项②是正确的,由此可得本题的答案.
解答:因为当
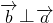 且
且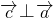 时,有
时,有 =0,但不能得出
=0,但不能得出 的结论,故①不正确;
的结论,故①不正确;由
 ,可得
,可得 -
- =0,即
=0,即 =
= ,所以
,所以 成立,故②正确;
成立,故②正确;因为
 =λ
=λ ,是一个与
,是一个与 共线的向量,而
共线的向量,而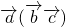 =μ
=μ ,是一个与
,是一个与 共线的向量.
共线的向量.所以等式
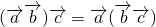 不一定成立,故③不正确;
不一定成立,故③不正确;∵
 ,θ是两向量的夹角
,θ是两向量的夹角∴由
 可得cosθ=1,可得θ=0.说明向量
可得cosθ=1,可得θ=0.说明向量 、
、 共线且同向,不一定相等,故④不正确.
共线且同向,不一定相等,故④不正确.故正确的选项只有②,1个
故答案为:A
点评:本题以命题的真假判断为载体,着重考查了平面向量的数量积运算、模的运算性质和平面向量基本定理等知识,属于基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 ;②
;②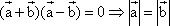 ;③
;③ ;④
;④ ,其中正确的结论有
,其中正确的结论有 ;②
;②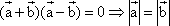 ;③
;③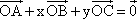
 ;④
;④ ;⑤
;⑤ ,其中正确的结论有
,其中正确的结论有