题目内容
如图,椭圆的方程为 ,其右焦点为F,把椭圆的长轴分成6等分,过每个等分点作x轴的垂线交椭圆上半部于点P1,P2,P3,P4,P5五个点,且|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5
,其右焦点为F,把椭圆的长轴分成6等分,过每个等分点作x轴的垂线交椭圆上半部于点P1,P2,P3,P4,P5五个点,且|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5 .
.(1)求椭圆的方程;
(2)设直线l过F点(l不垂直坐标轴),且与椭圆交于A、B两点,线段AB的垂直平分线交x轴于点M(m,0),试求m的取值范围.

【答案】分析:(1)由题意,知P1与P5,P2与P3分别关于y轴对称,设椭圆的左焦点为F1,从而|P1F|+|P5F|=|P1F|+|P1F1|=2a,|P2F|+|P3F|=2a,|P3F|=a,利用|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5a=5 ,即可求得椭圆的方程;
,即可求得椭圆的方程;
(2)设l的方程为y=k(x-1)(k≠0),代入椭圆方程 ,利用韦达定理,确定AB的中点的坐标,求出线段AB的垂直平分线方程,表示出m,即可确定m的取值范围.
,利用韦达定理,确定AB的中点的坐标,求出线段AB的垂直平分线方程,表示出m,即可确定m的取值范围.
解答:解:(1)由题意,知P1与P5,P2与P3分别关于y轴对称
设椭圆的左焦点为F1,则|P1F|+|P5F|=|P1F|+|P1F1|=2a,同时|P2F|+|P3F|=2a而|P3F|=a
∴|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5a=5
∴a=
∴椭圆的方程为 ;
;
(2)由题意,F(1,0),设l的方程为y=k(x-1)(k≠0),代入椭圆方程
消元整理,得(1+2k2)x2-4k2x+2k2-2=0
设A(x1,y1),B(x2,y2),AB的中点为(x,y),
则
∴线段AB的垂直平分线方程为y-y=- (x-x)
(x-x)
令y=0,得m=x+ky= =
= =
=
由于 ,∴
,∴
∴0<m< .
.
点评:本题考查椭圆的标准方程,考查椭圆的对称性,考查韦达定理的运用,求出线段AB的垂直平分线方程是关键.
 ,即可求得椭圆的方程;
,即可求得椭圆的方程;(2)设l的方程为y=k(x-1)(k≠0),代入椭圆方程
 ,利用韦达定理,确定AB的中点的坐标,求出线段AB的垂直平分线方程,表示出m,即可确定m的取值范围.
,利用韦达定理,确定AB的中点的坐标,求出线段AB的垂直平分线方程,表示出m,即可确定m的取值范围.解答:解:(1)由题意,知P1与P5,P2与P3分别关于y轴对称
设椭圆的左焦点为F1,则|P1F|+|P5F|=|P1F|+|P1F1|=2a,同时|P2F|+|P3F|=2a而|P3F|=a
∴|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5a=5

∴a=

∴椭圆的方程为
 ;
;(2)由题意,F(1,0),设l的方程为y=k(x-1)(k≠0),代入椭圆方程

消元整理,得(1+2k2)x2-4k2x+2k2-2=0
设A(x1,y1),B(x2,y2),AB的中点为(x,y),
则

∴线段AB的垂直平分线方程为y-y=-
 (x-x)
(x-x)令y=0,得m=x+ky=
 =
= =
=
由于
 ,∴
,∴
∴0<m<
 .
.点评:本题考查椭圆的标准方程,考查椭圆的对称性,考查韦达定理的运用,求出线段AB的垂直平分线方程是关键.

练习册系列答案
相关题目
 如图,椭圆的方程为
如图,椭圆的方程为 ,其右焦点为F,把椭圆的长轴分成6等分,过每个等分点作x轴的垂线交椭圆上半部于点P1,P2,P3,P4,P5五个点,且|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5
,其右焦点为F,把椭圆的长轴分成6等分,过每个等分点作x轴的垂线交椭圆上半部于点P1,P2,P3,P4,P5五个点,且|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5 .
.
 如图,椭圆的方程为
如图,椭圆的方程为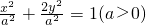 ,其右焦点为F,把椭圆的长轴分成6等分,过每个等分点作x轴的垂线交椭圆上半部于点P1,P2,P3,P4,P5五个点,且|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5
,其右焦点为F,把椭圆的长轴分成6等分,过每个等分点作x轴的垂线交椭圆上半部于点P1,P2,P3,P4,P5五个点,且|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5 .
.