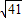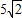题目内容
若△ABC的角A,B,C对边分别为a、b、c,且a=1,∠B=45°,S△ABC=2,则b=( )
| A、5 | ||
| B、25 | ||
C、
| ||
D、5
|
分析:先利用三角形面积公式求得c的值,进而利用余弦定理,求得b.
解答:解:S△ABC=
acsinB=
c•
=2,c=4
∴b=
=
=5
故选A
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |
∴b=
| a2+c2-2accosB |
1+32-2×4
|
故选A
点评:本题主要考查了正弦定理和余弦定理的应用.在解三角形问题中,一般利用正弦定理或余弦定理完成边和角的转换.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
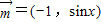 ,
,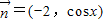 ,函数
,函数 .
.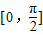 上的最大值;
上的最大值;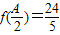 ,
,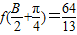 ,a+b=11,求a的值.
,a+b=11,求a的值.