题目内容
试问:当且仅当a,b满足什么条件时,对椭圆C1:
答案:
解析:
解析:
解:如图所示,圆外切平行四边形一定是菱形,圆心即菱形中心,所求条件为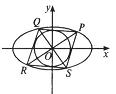
必要性的证明: 设椭圆C1上任意一点P(r1cosθ,r1sinθ),所以有Q(r2cos(θ+ 其中|OP|=r1,|OQ|=r2,代入椭圆方程中,得
又菱形PQRS与单位圆C0外切,所以Rt△POQ斜边PQ上的高h=1。而
充分性的证明:设 设|OP|=r1,|OQ|=r2,则P的坐标为(r1cosθ,r1sinθ),Q的坐标为(r2cos(θ+ 代入椭圆方程,得
又在Rt△POQ中,斜边PQ上的高h=1,则h= = ∴ 同理,点O到QR,RS,SP的距离都是1,所以菱形PQRS与单位圆C0外切。 |

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
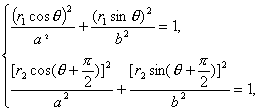
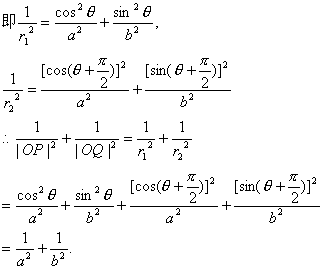
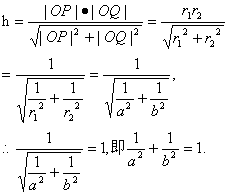
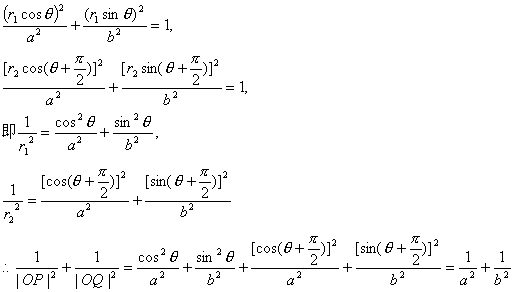
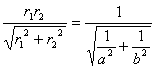
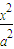 +
+ =1 (a>b>0).试问:当且仅当a,b满足什么条件时,对C1上任意一点P,均存在以P为顶点,与C外切,与C1内接的平行四边形?并证明你的结论.
=1 (a>b>0).试问:当且仅当a,b满足什么条件时,对C1上任意一点P,均存在以P为顶点,与C外切,与C1内接的平行四边形?并证明你的结论.