题目内容
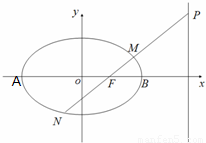 已知A,B是椭圆
已知A,B是椭圆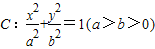 的左,右顶点,B(2,0),过椭圆C的右焦点F的直线交椭圆于点M,N,交直线x=4于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
的左,右顶点,B(2,0),过椭圆C的右焦点F的直线交椭圆于点M,N,交直线x=4于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点(1)求椭圆C的方程;
(2)求三角形MNT的面积的最大值.
【答案】分析:(1)由题设知a=2,b=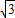 .由此能求出椭圆C的方程.
.由此能求出椭圆C的方程.
(2)由点差法知PQ的中垂线交x轴于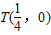 ,设M(x1,y1),N(x2,y2),直线MN:x=my+1与椭圆联立可得(3m2+4)y2+6my-9=,0
,设M(x1,y1),N(x2,y2),直线MN:x=my+1与椭圆联立可得(3m2+4)y2+6my-9=,0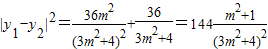 ,由此能求出三角形MNT的面积的最大值.
,由此能求出三角形MNT的面积的最大值.
解答:解:(1)由题设知a=2,b=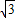
椭圆C的方程
(2)由点差法知PQ的中垂线交x轴于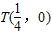
设M(x1,y1),N(x2,y2),直线MN:x=my+1与椭圆联立可得(3m2+4)y2+6my-9=0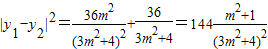
令t=m2+1≥1,则
故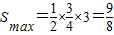
点评:本题考查椭圆C的方程,求△MNT的面积的最大值.解题时要认真审题,仔细解答,注意椭圆性质的合理运用.
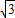 .由此能求出椭圆C的方程.
.由此能求出椭圆C的方程.(2)由点差法知PQ的中垂线交x轴于
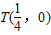 ,设M(x1,y1),N(x2,y2),直线MN:x=my+1与椭圆联立可得(3m2+4)y2+6my-9=,0
,设M(x1,y1),N(x2,y2),直线MN:x=my+1与椭圆联立可得(3m2+4)y2+6my-9=,0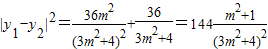 ,由此能求出三角形MNT的面积的最大值.
,由此能求出三角形MNT的面积的最大值.解答:解:(1)由题设知a=2,b=
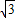
椭圆C的方程

(2)由点差法知PQ的中垂线交x轴于
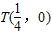
设M(x1,y1),N(x2,y2),直线MN:x=my+1与椭圆联立可得(3m2+4)y2+6my-9=0
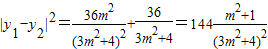
令t=m2+1≥1,则

故
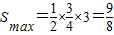
点评:本题考查椭圆C的方程,求△MNT的面积的最大值.解题时要认真审题,仔细解答,注意椭圆性质的合理运用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
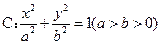 的左,右顶点,
的左,右顶点, ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线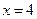 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
 的左,右顶点,
的左,右顶点,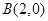 ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线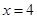 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点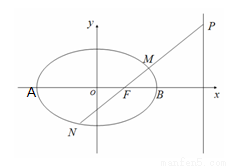

 已知A,B是椭圆
已知A,B是椭圆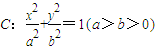 的左,右顶点,B(2,0),过椭圆C的右焦点F的直线交椭圆于点M,N,交直线x=4于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
的左,右顶点,B(2,0),过椭圆C的右焦点F的直线交椭圆于点M,N,交直线x=4于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点