题目内容
设P是双曲线分析:若设出P点坐标,把|PA|+|PF|表示出来,再求最值相当困难.画出图形,联想双曲线的定义,则可使问题迎刃而解.
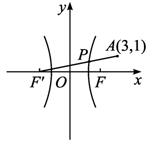
解:设F′为双曲线的左焦点,
则|PF′|-|PF|=2![]() ,|PF|=|PF′|-2
,|PF|=|PF′|-2![]() ,
,
∴|PA|+|PF|=|PA|+|PF′|-2![]() ,原问题转化成了求|PA|+|PF′|的最小值问题,(如图)(|PA|+|PF′|)min=|AF′|=
,原问题转化成了求|PA|+|PF′|的最小值问题,(如图)(|PA|+|PF′|)min=|AF′|=![]() .
.
∴ (|PA|+|PF|)min=(|PA|+|PF′|)min-2![]() =
=![]() -2
-2![]() .
.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目

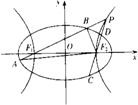 如图,已知椭圆
如图,已知椭圆