题目内容
随机变量X的分布列如下:
| ξ | -1 | 0 | 1 |
| P | a | b | c |
 ,则
,则 的值是
的值是
5
解析试题分析:根据题意,由于解:∵a,b,c成等差数列,∴2b=a+c,∵a+b+c=1, Eξ=-1×a+1×c=c-a=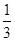
联立三式得a=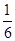 ,b=
,b=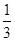 ,c=
,c=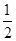 ,故可知
,故可知 =9D(X)=
=9D(X)=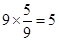 ,故可知结论为5.
,故可知结论为5.
考点:离散型随机变量的期望和方差
点评:这是一个综合题目,包括等差数列,离散型随机变量的期望和方差,主要考查分布列和期望的简单应用,通过解方程组得到要求的变量,这与求变量的期望是一个相反的过程,但是两者都要用到期望的公式.

练习册系列答案
相关题目
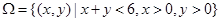 ,
, ,若向区域
,若向区域 上随机投掷一点
上随机投掷一点 ,则点
,则点 的概率为 .
的概率为 . (各学校是否录取他相互独立,允许他可以被多个学校同时录取).则此同学至少被两所学校录取的概率为_____.
(各学校是否录取他相互独立,允许他可以被多个学校同时录取).则此同学至少被两所学校录取的概率为_____.